Zwei kleine Übungen, Farben in Bewegung zu versetzen. Oben: »Ohne Titel«, Acryl auf Leinwand 40×50 cm. Unten: »Altrhein« , Acryl auf Leinwand-Karton 24×30 cm.
Autor: HorstTh
Antennen-Analysator FA-VA5 und Smith-Diagramm
Zu diesem Thema habe ich einige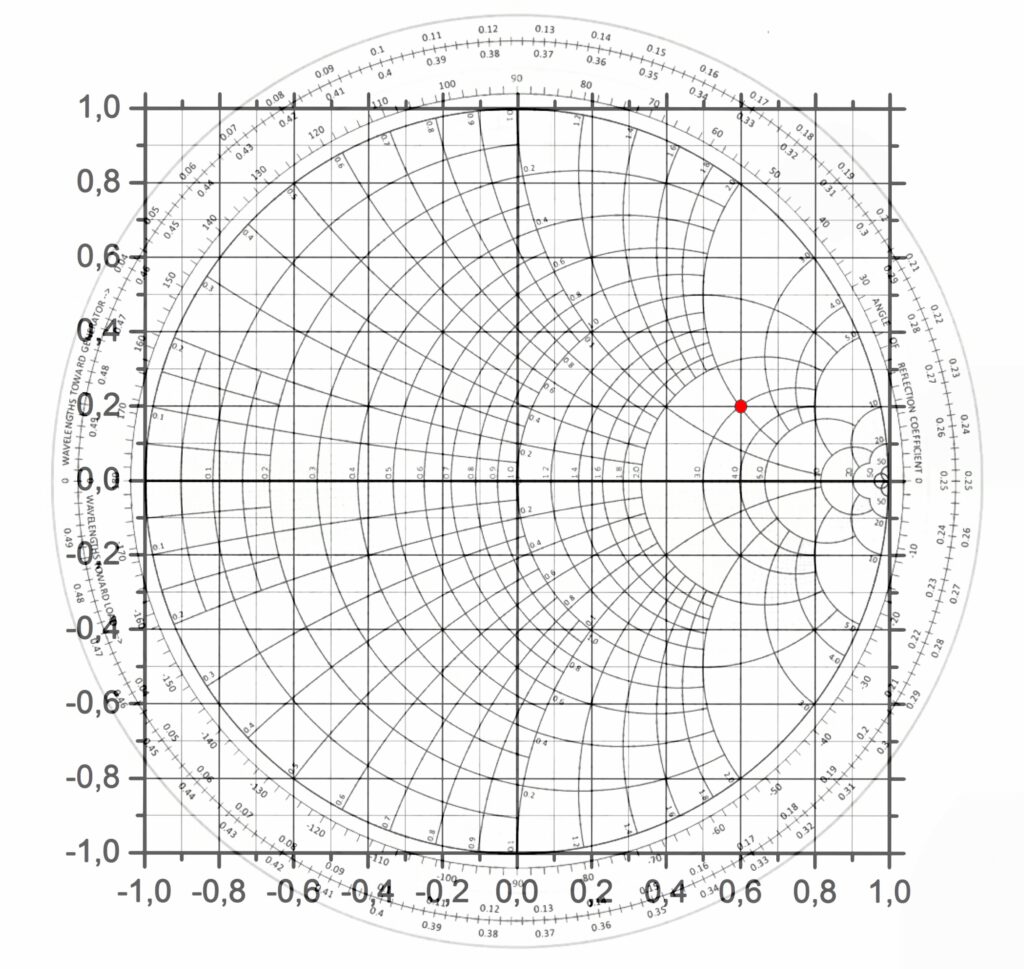 
Erläuterungen zusammengestellt, gedacht als Kurs für die Funkamateure des DARC-Ortsverbands Mönchengladbach. Wer hineinschauen möchte, klicke hier.
Der Reflexionsfaktor, den der Antennen-Analysator misst, wird gerne in einer Art »Schnittmusterbogen«, genannt Smith-Diagramm, dargestellt. Die Abbildung zeigt ein solches Diagramm und – überlagert – ein kartesisches Koordinatensystem.
Smith-Diagramm mit überlagertem kartesischen Koordinatensystem. Im kartesischen System sind Real- und Imaginärteil des Reflexionsfaktors Γ (Gamma) ablesbar. Beispiel: Der (rote) Punkt Γ = 0.6 + j0.2. Er ist das Abbild der (normierten) Impedanz z = 3 + j2 und liegt deshalb im Smith-Diagramm auf dem Schnittpunkt der Kreise Re(z) = 3 und Im(z) = 2. In der Praxis sind die Werte Re(Γ) = 0.6 und Im(Γ) = 0.2 nur Rechengrößen. Deshalb wird das kartesische Koordinatensystem nie gezeigt.
Schnee im Hohen Venn
Es hatte geschneit im Hohen Venn als wir am Wochenende von Nahtsief (Bushaltestelle) bis Baraque Michel wanderten. Links ein »Moorauge« bei Nahtsief, rechts ein Blick aufs Wallonische Venn.
Klever Fluchtlinien (Nachtrag)
In den »Klever Fluchtlinien« ging es um des Test eines Computerprogramms, das (zentral-)perspektivische Darstellungen in einer Bildebene (Leinwand oder Zeichenkarton) berechnet. Der Blick vom Obelisken auf dem Klever Springenberg in Richtung Hoch Elten war dasTestobjekt: Die Perspektive entlang dieser Sichtachse sollte vom Computerprogramm wiedergegeben werden. Das war auch der Fall: Der »vanishing point« der Fluchtlinien lag genau dort, wo er geografisch liegen sollte – wenige Meter unterhalb der Kirche St. Vitus in Hoch Elten.
Den Eltener Hügel mit der Kirche habe ich vor einigen Tagen besucht. Dort ist die Skulptur »Stein Tor« des Bildhauers Christoph Wilmsen-Wiegmann nicht zu übersehen: Zwei riesige, parallel aufgestellte Basaltpfeiler lassen einen schmalen Spalt offen, hinter dem, aus Richtung Kleve betrachtet, der Kirchturm von St. Vitus erscheint. Das also ist er – der »Fluchtpunkt«. Dazu, im Boden eingelassen, ein länglicher Steinquader, der die Richtung der Sichtachse markiert.
Die Achse ist übrigens eine grenzüberschreitende Europäerin: sie durchquert niederländisches und deutsches Gebiet. Die acht Kilometer lange Sichtstrecke ist außerdem durch eine Reihe von Skulpturen kulturell aufgeladen.
Eine Übung in Farbe
Im Lenbach-Haus (München) betrachte ich Corots Studie »Der Grosse Baum«. Die verhüllten Farben sind eine Alternative zu meinen Landschaftsgemälden in Grün und Blau – von meiner Lehrerin mit Recht kritisiert. Also hier eine Übung zu Corots Studie – ohne den Baum, nur der Hintergrund mit dem Dorf am See.
Übung nach Corots Studie »Der Große Baum«, Acryl auf Leinwand 40 x 50
Corot: Studie »Der Große Baum«, Lenbachhaus München
3 Voltmeter . . .
… messen den Wechselstromwiderstand eines Schwingkreises. Elektromagnetische Schwingkreise waren immer schon mein Lieblingsspielzeug als Hobby-Physiker. Dabei sind sie wenig kooperativ, Theorie und Experiment stimmen nicht immer überein. Hier ein Beispiel:
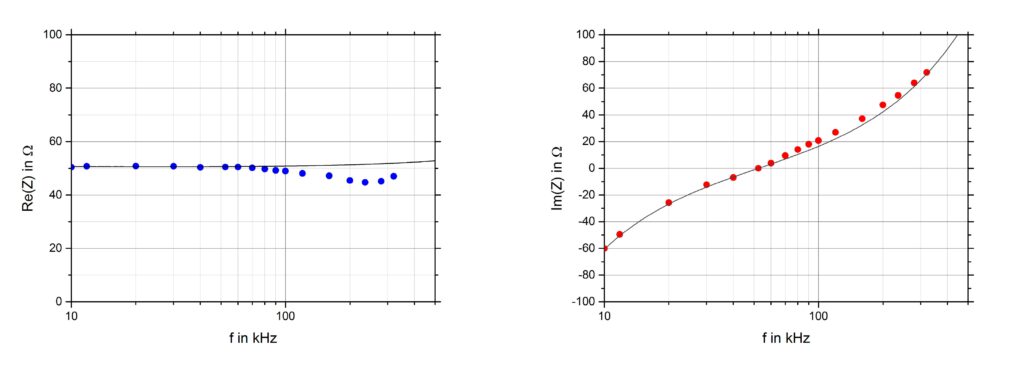
Ich messe die Impedanz (den Wechselstromwiderstand) eines Serien-Schwingkreises, bestehend aus Spule, Kondensator und Ohmschem Widerstand, und zwar mit der so genannten 3-Voltmeter-Methode. Dazu benutzt man in der Regel Effektivwertmesser (»AC true-rms«) mit hohem Eingangswiderstand. Die Methode liefert bei geduldigem Messen die Impedanz getrennt nach Realteil (blaue Punkte, linkes Diagramm) und Imaginärteil (rote Punkte, rechtes Diagramm) – und zwar in Abhängigkeit von der Frequenz der anliegenden Spannung. Unabhängig davon bestimme
ich den Frequenzgang derselben Größe (der Impedanz) mit Hilfe eines Vektor-Antennen-Analysators. Das Ergebnis dieser Messung sind die ausgezogenen Kurven in den Diagrammen. Man erkennt, dass Punkte und Kurven zwar demselben Trend folgen, zum Teil aber voneinander abweichen. Ich vertraue den Daten des Antennen-Analysators mehr als den mit dem Voltmeter gemessenen. Wo liegt der Fehler? Also ist wieder einmal Nachdenken angesagt.
Hier eine ausführliche Beschreibung der Messung.
BoA in der Nacht + 2
Zwei Gemälde mit Motiven, die mein(e) »BoA-in-der-Nacht« ergänzen: Die »Grube« (Abhang einer Braunkohlengrube) und das »Umspannwerk«. Schon lange geplant, jetzt fertiggestellt. Hier das Trio in Gesamtsicht. Alle Gemälde 40 x 50 Acryl auf Leinwand.
»Grube« »BoA-in-der-Nacht« »Umspannwerk«
(BoA = Braunkohlenkraftwerk mit optimierter Anlagentechnik)
Herbst
Fotos einer Wanderung von Ahrweiler nach Rheinbach. Gesättigte Herbstfarben trotz des trüben Wetters.
Farbstift-Übung
»Moritzburg« (Weiher des Schlosses Moritzburg bei Dresden), Farbstift auf Papier 20×28 cm
Verschiebungsstrom . . . ?
Im Physikunterricht hätte ic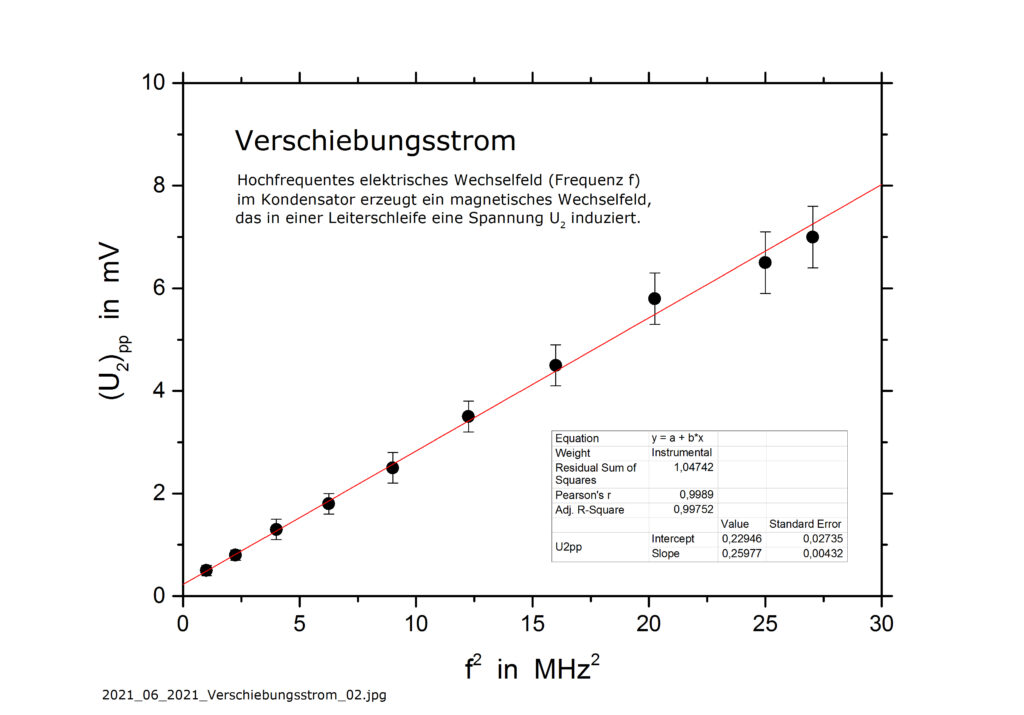
h den Versuch gerne vorgeführt: den (mehr oder weniger) direkten Nachweis des Verschiebungsstroms (engl. displacement current) in einem Kondensator. Offenbar war ich nicht clever genug, mir eine passende Messanordnung zu überlegen. Denn das Experiment, das Sanyal und Chakrabarty1 vorschlagen, ist verblüffend einfach konzipiert und problemlos aufzubauen. Die von den Autoren angegebenen Messdaten stimmen jedoch nicht mit der Theorie überein. Eine Begründung dafür wird genannt, ist aber zum Teil unbefriedigend. Ich habe deshalb versucht, das Experiment nachzubauen und eigene Messungen auszuführen.
Um die Existenz des Verschiebungsstroms im Kondensator nachzuweisen, muss man zeigen, dass eine zeitliche Änderung des elektrischen Feldes zwischen den Kondensatorplatten ein Magnetfeld erzeugt. Die Idee ist, dieses Magnetfeld durch Induktion nachzuweisen: Man lässt die Feldlinien des Magnetfeldes durch eine Leiterschleife hindurchtreten und damit in der Leiterschleife eine Spannung induzieren.
Das Ergebnis meiner Messungen zeigt die Abbildung: Aufgetragen ist die in der Leiterschleife induzierte Spannung (Spitze-Spitze-Wert (U2)pp) als Funktion des Quadrats der Frequenz f. Die Messpunkte liegen, wie von der Theorie vorhergesagt, auf einer Geraden durch den Nullpunkt (jedenfalls näherungsweise durch den Nullpunkt). Ihre Steigung ist aber größer als der theoretisch berechnete Wert. Das ist dasselbe Ergebnis wie das von Sanyal und Chakrabarty: U2 ist proportional zu f 2, jedoch ist der Proportionalitätsfaktor um eine Größenordnung (bei Sanyal und Chakrabarty sind es zwei Größenordnungen) größer als theoretisch berechnet. Also keine neuen Erkenntnisse – leider. Ob sich das Experiment als Nachweis des Verschiebungsstroms eignet, ist also fraglich. Mehr dazu hier.
1 G.S. Sanyal und Ajay Chakrabarty: A Direct Experimental Proof of Displacement Current. Resonance volume 13, pages 1065–1073 (2008) , https://doi.org/10.1007/s12045-008-0126-6