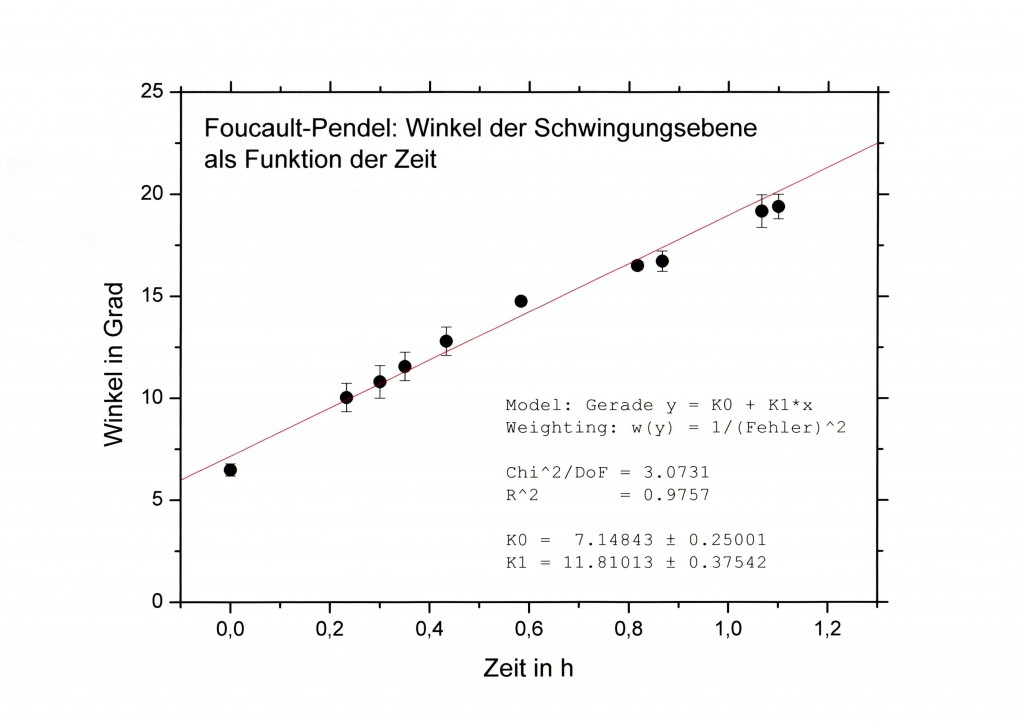
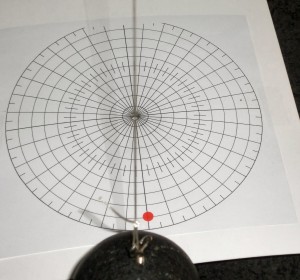
Im Artikel Foucault-Pendel fehlten Details zum Versuchsaufbau und zum eigentlichen Experiment. Die sollten nachgeliefert werden. Daraus wird leider nichts, die Unterlagen sind verschollen. Deshalb habe ich das Pendel noch einmal aufgebaut – in der gleichen Anordnung wie vor einigen Jahren. Die elektronische Steuerung funktionierte zwar nach einigen Eingriffen, aber das Pendel dachte nicht daran, seine Schwingungsebene zu verändern. Der Grund dafür, vermutete ich, war das Stahlseil, das ich als Pendelaufhängung benutzte (zu starr, zu sehr verdrillt, oder …?). Mit einem Kunststoffseil drehte sich die Schwingungsebene wieder – aber dafür verlängerte sich das Seil während des Experiments. Nach etwa drei Stunden streifte der Magnet an der Unterseite der Pendelkugel den Eisenkern der Antriebsspule. Damit fand die Schwingung ein jähes Ende. Immerhin ergab eine erste Messung (über ein Zeitintervall von ca. einer Stunde) den richtigen Wert für die Präzessionsrate (Abb. unten). Sie betrug 11,8 ± 0,4 Grad/Stunde – der theoretische Wert ist 11,7 Grad/Stunde. Also ein bescheidener Erfolg. Die Abbildung links oben zeigt das Pendel mit einem darunter angebrachten Winkelmesser. Mit etwas Geduld und einer ruhigen Hand gelingt es, die optische Achse der Kamera in die Schwingungsebene des Pendels zu bringen. Dann markiert der Pendelfaden auf dem Foto den momentanen Winkel der Schwingungsebene.
Zum Schluss zwei Bemerkungen zur Theorie: (1) Die Herleitung der Formel für den Drehwinkel der Schwingungsebene eines Foucault-Pendels ist eine kleine Übung in Newtonscher Mechanik für rotierende Systeme. (2) Leider dreht sich die Schwingungsebene auch dann, wenn das Pendel nicht geradlinig schwingt, sondern eine elliptische Bahn durchläuft (Deshalb muss diese Bewegung gedämpft werden, zum Beispiel durch den Charron-Ring). Die Winkelgeschwindigkeit dieser „elliptischen“ Präzession ist proportional zum Flächeninhalt der Bahnellipse. Sie auszurechnen ist eine etwas umfangreichere mathematische Trainingseinheit.
