Beim Stöbern im Netz stoße ich auf das Stichwort »Wolfston«. Das Thema gibt leider nichts her für physikalische (Hobby-)Experimente, dazu benötigt man professionelles Equipment. Ich finde es aber interessant. Also schaue ich nach, was die Literatur zum »Wolf« zu sagen hat. Dabei ist einiges hängen geblieben, vielleicht ist es auch für Andere von Interesse.
Ein »Wolf« ist der jaulende, flatterhafte Ton, den eine Geige, ein Cello oder ein anderes Saiteninstrument beim Spielen einer bestimmten Note erzeugt. Er entsteht, so liest man, wenn der Korpus des Instruments in Resonanz mitschwingt und eine Schwebung mit dem gespielten Ton hervorruft. Der Resonanzkörper ist für ein Saiteninstrument unerlässlich: Eine gestrichene oder gezupfte Saite wäre ohne ihn nicht hörbar. Mehr über die Korpusresonanzen einer Geige hier.
Eine Geige wird offenbar nur selten von einem Wolf befallen, bei einem Cello aber stört er. Man unterdrückt ihn, indem man auf dem Teil der Saite zwischen Steg und Saitenhalter (der »Nachlänge« der Saite) eine kleine Zusatzmasse anbringt. Sie wiegt einige Gramm und besteht beispielsweise aus einem Metallröhrchen, das innen mit einer Gummi-Manschette ausgekleidet ist und mit einer Schraube auf der Nachlänge befestigt wird (Foto). Das winzige Gebilde hat den Namen »Wolftöter«, weniger gewalttätig klingt »Wolfstimmer«.
 Aus der Literatur entnehme ich, dass der Wolfstimmer im Prinzip ein raffiniert abgestimmter mechanischer Schwingungstilger ist (engl. »Tuned Mass Damper«). Dieses rein theoretische Objekt hat mit dem Metallröhrchen auf der Saiten-Nachlänge zunächst nichts zu tun. Ein mechanischer Schwingungstilger besteht aus zwei Massen, einer größeren und einer kleineren. Die größere ist die der »Struktur«, deren Bewegung (»Schwingung«) gedämpft werden soll. Die kleinere Masse ist der Dämpfer oder »Tilger«. Struktur und Tilger sind durch eine Schraubenfeder elastisch gekoppelt und schwingen mit fast gleicher Frequenz. Parallel zur Schraubenfeder wirkt ein Dämpfungszylinder, dessen Dämpfungsgrad so eingestellt wird, dass die Schwingungsamplitude der Struktur stark vermindert wird: Ihre Resonanzkurve hat statt des üblichen Peaks ein flaches Dach niedriger Höhe, oft mit einer kleinen Einsattelung. Der Zwei-Massen-Schwingungstilger ist ein interessantes Thema der Schwingungslehre. Ich habe ihn einmal Schritt für Schritt durchgerechnet. Hier mehr darüber.
Aus der Literatur entnehme ich, dass der Wolfstimmer im Prinzip ein raffiniert abgestimmter mechanischer Schwingungstilger ist (engl. »Tuned Mass Damper«). Dieses rein theoretische Objekt hat mit dem Metallröhrchen auf der Saiten-Nachlänge zunächst nichts zu tun. Ein mechanischer Schwingungstilger besteht aus zwei Massen, einer größeren und einer kleineren. Die größere ist die der »Struktur«, deren Bewegung (»Schwingung«) gedämpft werden soll. Die kleinere Masse ist der Dämpfer oder »Tilger«. Struktur und Tilger sind durch eine Schraubenfeder elastisch gekoppelt und schwingen mit fast gleicher Frequenz. Parallel zur Schraubenfeder wirkt ein Dämpfungszylinder, dessen Dämpfungsgrad so eingestellt wird, dass die Schwingungsamplitude der Struktur stark vermindert wird: Ihre Resonanzkurve hat statt des üblichen Peaks ein flaches Dach niedriger Höhe, oft mit einer kleinen Einsattelung. Der Zwei-Massen-Schwingungstilger ist ein interessantes Thema der Schwingungslehre. Ich habe ihn einmal Schritt für Schritt durchgerechnet. Hier mehr darüber.
Inwiefern das Prinzip des Schwingungstilgers bei einem Saiteninstrument zur Anwendung kommt, ist in einem Artikel von Gidion1 erläutert. Soweit ich diesen verstanden habe, verscheucht man den Wolf wie folgt: Man erzeugt beim Spielen des zum Wolf neigenden Tons eine weitere Schwingung, deren Frequenz nur wenige Hertz neben der Wolfsresonanz liegt (der Korpusresonanz, die beim Wolf mitschwingt). Dazu stimmt man die Nachlänge der Saite, auf der sich der Wolfstimmer befindet, auf diese Frequenz ab. Bei einer Geige haben die zum Wolf tendierenden Resonanzen Frequenzen zwischen 450 und 550 Hz. Der Wolfstimmer ist in der Regel auf der Nachlänge der G-Saite angebracht. Die Saite selbst schwingt mit der Grundfrequenz 196 Hz. Ihre Nachlänge beträgt etwa 1/6 der Saitenlänge und schwingt daher mit sechsfach höherer Frequenz. Das sind 1176 Hz (und damit zwei Oktaven und eine Quinte höher als 196 Hz, denn 196×22×(3/2) Hz = 1176 Hz). Der Wolfstimmer senkt diese (Resonanz-)Frequenz beträchtlich, so dass man so in den Bereich um 500 Hz gelangt. Mit etwas Glück trifft man die Frequenz, die den Wolf dämpft.
Ein Beispiel dafür liefert Schleske2: Er regt die Korpusschwingungen einer Geige durch seitliches Klopfen gegen den Steg an, misst deren Intensität und zerlegt das registrierte Signal nach Fourier. Das Spektrum zeigt zwei Peaks bei etwa 430 und 510 Hz, einmal ohne, das andere Mal mit Wolfdämpfer. (Die ebenfalls sichtbaren Resonanzen oberhalb 1000 Hz interessieren hier nicht.) Deutlich erkennbar ist: Der 510-Hz-Peak wird im Bereich seines Schwerpunkts durch den Dämpfer scharfkantig3 »aufgeschlitzt«. Die Intensität geht an dieser Stelle um etwa zwei Zehnerpotenzen (–20 dB) zurück. Die Absenkung der Resonanzfrequenz einer schwingenden Saite durch die fast punktförmige Masse des Wolfstimmers ist ein weiteres physikalisches Phänomen, mehr darüber hier.
Bemerkungen zum Foto: (1) Der Wolfstimmer auf der G-Saite meiner Geige ist eigentlich überflüssig, er sitzt dort nur des Fotos wegen. (2) Erst vor kurzem ist mir aufgefallen: die Nachlänge der Saiten ist kürzer als normal. Ich habe das Instrument vor Jahren als leicht beschädigte, aber wieder instandgesetzte Geige gekauft. Bei der Reparatur wurde vermutlich der Saitenhalter einer Bratsche eingebaut.
1 Gidion, G.: Akustische Resonatoren zur Analyse und Kontrolle von Schwingungsfähigen Systemen am Beispiel von Streichinstrumenten und Dielektrischen Elastomeraktoren, https://publishup.uni-potsdam.de › index › index › docId
2 Schleske, M.: Auf Wolftonjagd, Auszug aus: Handbuch Geigenakustik der website www.schleske.de (2003)
3 Die Kurve erinnert an den Frequenzgang eines Notch-Filters (Elektrotechnik).
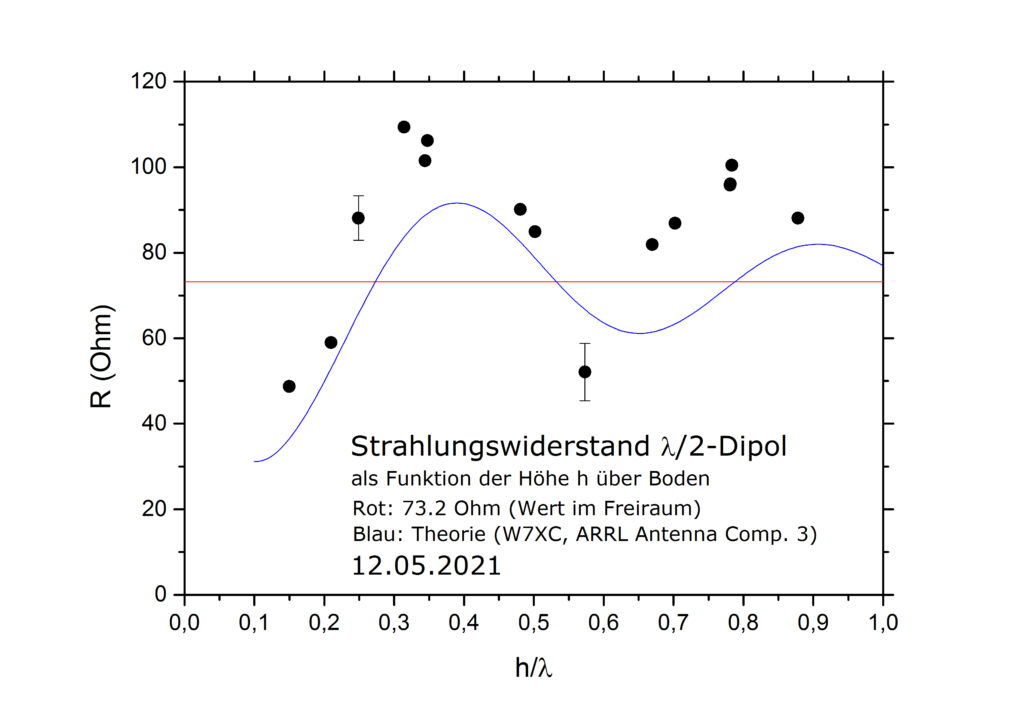
 Abbildung 1 Foto der Antenne. Der Holzrahmen
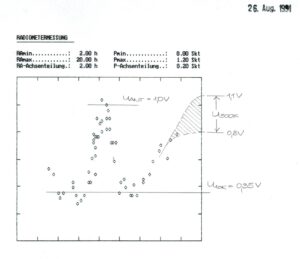
Abbildung 1 Foto der Antenne. Der Holzrahmen 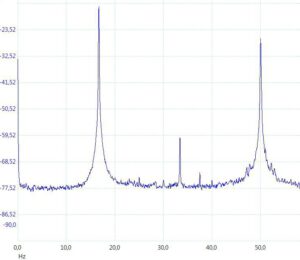 Abbildung 2 Spektrum des Antennenrauschens meiner Loop
Abbildung 2 Spektrum des Antennenrauschens meiner Loop 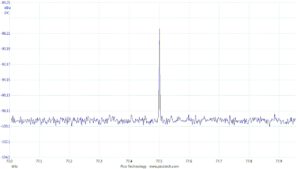 Abbildung 3 Ausschnitt aus dem Empfangsspektrum der Loop
Abbildung 3 Ausschnitt aus dem Empfangsspektrum der Loop