Kategorie: Computergrafik

Berechnung der Feigenbaumkonstante

 in Computergrafik

Die Feigenbaumkonstante ist eine universale Konstante der mathematischen Logistik. Ihr „Entdecker“ und Namensgeber ist der US-amerikanische Physiker Mitchell Jay Feigenbaum. Es geht um das Verhalten der Iterationen xn+1 = fr(xn) der logistischen Funktion fr(xn) = rxn(1 – xn). Der Verlauf der Grenzwerte von xn+1 = fr(xn) für n→unendlich, aufgetragen in Abhängigkeit des Parameters r, heißt Bahn der logistischen Funktion. Abbildung 1 zeigt diese Bahn für 1 < r < 4. Sie zeichnet sich dadurch aus, dass sie an der Stelle r = 3 in zwei Gabelzinken aufspaltet und diese Aufspaltung (Bifurkation) sich bei höheren Werten von r mehrmals fortsetzt. Bei jeder Gabelung verdoppelt sich die Anzahl der Äste (Perioden) der Bahn und die Bifurkationsstellen rücken näher aufeinander zu. Bei etwa r = 3,56 geht die Bahn in ein Gebiet über, in dem sie viele unregelmäßige Werte annimmt. Dieses ist das Gebiet des Chaos.

 

 

 

 

 

 

 

 

 

 

 

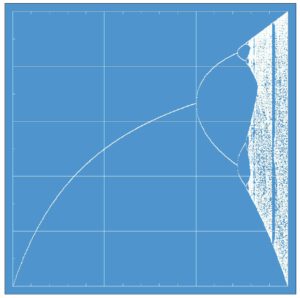
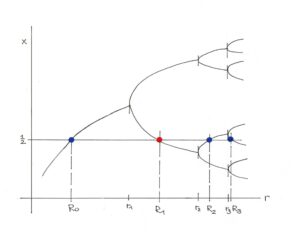
Abbildung 1: Bahn der logistischen Funktion im Intervall [1,4]. Die Bahn ist der Grenzwert der Iteration xn+1 = fr(xn) für n→unendlich. Er ist in y-Richtung aufgetragen. In x-Richtung steht als unabhängige Größe der Parameter r. Die Bahnwerte beginnen sich bei r = 3 in zwei Gabelzinken aufzuspalten. Diese Aufspaltung (Bifurkation) erfolgt danach mehrmals – bis bei etwa r = 3,56 das Chaos erreicht wird.

Die Werte ri der ersten Bifurkationsstellen sind in Tabelle 1 in Spalte 2 aufgeführt. Für i→unendlich streben sie gegen einen Grenzwert, der Feigenbaumpunkt heißt. Er liegt in etwa dort, wo das Chaos einsetzt. Die Feigenbaumkonstante δ hingegen ist der Grenzwert der Quotienten  δi = (ri+1 – ri)/(ri+2 – ri+1) für i →unendlich. Spalte 3 der Tabelle 1 zeigt die Quotienten δi für i ≤ 5. Die Zahl δ4 = 4,6686…. kommt dem Grenzwert der Feigenbaumkonstante schon recht nahe.


Tabelle 1
=============================
   i      ri          δi-1
————————————————————————————–
   1   3,0000000    –
   2   3,4494897   4,7514
   3   3,5440903   4,6562
   4   3,5644073   4,6683
   5   3,5687594   4,6686
=============================   

 

Der genaue Grenzwert δ  lässt sich nur mit einem Näherungsverfahren bestimmen – eine mathematisch aufwändige Sache. Feigenbaum war genial: er benutzte einen einfachen Taschenrechner um ihren Wert zu berechnen. Wir nehmen dazu einen Computer zur Hand.

 

 

 

 

 

 

 


Abbildung 2:  Schematische Skizze der Bahn. Die Bifurkationsstellen sind mit r1,r2,r3, … bezeichnet.
Zur Berechnung der Feigenbaumkonstanten benutzt man die Werte der superstabilen Stellen R1, R2, R3, … .

 

Das Näherungsverfahren benutzt die Tatsache, dass es zwischen zwei Bifurkationsstellen immer auch eine Stelle gibt, an denen die Iteration xn+1 = fr(xn) so genannte superstabile Fixpunkte besitzt. In Abbildung 2 sind diese Stellen mit R1,, R2, R3, … bezeichnet (die Bifurkationsstellen mit r1, r2, r3, …). Da die Werte der superstabilen Stellen zwischen jeweils zwei aufeinander folgenden Bifurkationsstellen eingeschlossen sind, haben beide Zahlenfolgen denselben Grenzwert. Zur Berechnung der Feigenbaumkonstante benutzt man die Werte der superstabilen Stellen R1,, R2, R3, … .

 

Tabelle 2
Näherungswerte für den Feigenbaumpunkt α (Spalte rN) und die Feigenbaumkonstante  δ (Spalte deltaN1).
Mit n werden die Näherungsschritte gezählt, nr ist die Anzahl der Versuche, den superstabilen Punkt zu treffen

==============================================
 n          rN          nr      deltaN1
—————————————————————————————————————————————-
  0   2,0000000000000            –
  1   3,2360679774998      4,0000000000000     
  2   3,4985616993277  6   4,7089430135405
  3   3,5546408627688  4   4,6807709980107
  4   3,5666673798563  4   4,6629596111141
  5   3,5692435316371  3   4,6684039259180
  6   3,5697952937499  3   4,6689537409485
  7   3,5699134654223  3   4,6691571814003
  8   3,5699387742333  2   4,6691910032120
  9   3,5699441946081  2   4,6691994611323
 10   3,5699453554865  2   4,6692011701107
 11   3,5699456041111  1   4,6692017591474
==============================================

 

Die Mathematik des Näherungsverfahrens – und insbesondere die Bedeutung der superstabilen Fixpunkte der Iteration xn+1 = fr(xn) – wird hier beschrieben. Das zugehörige (Java-)Computerprogramm ist nur wenige Zeilen lang. Seine numerische Genauigkeit beträgt etwa 10–14 . Mit dem Programm wurden die Näherungsschritte in Tabelle 2 berechnen. Der Literaturwert der Feigenbaumkonstante ist  δ = 4,669201609102990… . Man erkennt, dass die Näherungen bis etwa n = 10 dem Literaturwert zustreben, danach sich aber von ihm weg bewegen.

 

Literatur:
M. J. Feigenbaum, J. Stat. Phys. 19, 25 (1978).
M. J. Feigenbaum, J. Stat. Phys. 219, 665 (1978).
D. Kartofelev: Nonlinear Dynamics, Lecture Notes #11, Feigenbaum’s Analysis of Period Doubling,  
www.tud.ttu.ee/web/dmitri.kartofelev/YFX1560/LectureNotes_11.pdf.
J. H- Sylvester: Die logistische Abbildung, Das Feigenbaum-Szenario, Seminarvortrag,
www.math.uni-hamburg.de/home/lauterbach/scripts/seminar03/sylvester.
Hein-Otto Peitgen, Hartmut Jürgens und Dietmar Saupe: Fractals for the Classroom, New York, 1992,   Band 2, S. 224 ff.
N. Grzech: Die logistische Gleichung als ein Beispiel für chaotische Prozesse in der Physik, Examensarbeit, Universität Rostock,
www.wsf.uni-rostock.de/examensarbeit.pdf.

Mies van der Rohe in Krefeld

 in Computergrafik, Verschiedenes

Die bekanntesten Gebäude, die der Architekt Ludwig Mies van der Rohe entworfen hat, stehen in der Stadt Chicago (USA): das Kluczynski Federal Building, das Post Office, das 860–880 North Lake Shore Drive Building und die Crown Hall des Illinois Institutes of Technology. Sie alle sind quaderförmige Bauten, deren Fassaden sehr viel Glas enthalten. Das Glas schließt in der Regel bündig mit der Außenwand ab, so dass eine durchgehend glatte Oberfläche entsteht. Die Bauweise ist typisch für den sogenannten Internationalen Stil.

Der einzige von Mies van der Rohe entworfene Bau in Europa, der diese quaderartige Architektur aufweist, steht in Krefeld. Es ist das HE-Gebäude auf dem Gelände der ehemaligen Vereinigten Seidenwerke Krefeld (Verseidag). Da es ein perfekter Quader ist, eignet er sich gut, an ihm einige Grundaufgaben der Darstellenden Geometrie nachzuvollziehen. Das Fach »Darstellende Geometrie für Architekten« wird zwar heute noch an der Hochschule gelehrt, in der Praxis arbeitet man aber vermutlich mit der bequemeren CAD-Software.

Ich jedenfalls habe einmal spaßeshalber versucht, aus einem Foto des HE-Gebäudes (in Übereck-Ansicht) Grund- und Aufriss durch Zeichnung zu rekonstruieren. Das Ergebnis ist in Abbildung 1 zu sehen. Sie zeigt die beiden Risse in der sogenannten »Architekten-Anordnung«. Die (zeichnerische) Rekonstruktion ergibt ein Verhältnis (Länge : Breite) = 3,05, die TIM-online-Karte liefert (Länge : Breite) = 2,93 (56,47m : 19,28 m = 2,93). Das heißt, meine zeichnerische (Re-)Konstruktion kann nicht ganz falsch sein.

Abb. 1 Rekonstruktion: Grund- und Aufriss des HE-Gebäudes auf dem Gelände der ehemaligen Vereinigten Seidenwerke (Verseidag) in Krefeld. Das Gebäude ist der einzige Quaderbau, der nach dem Entwurf des Architekten Mies van der Rohe in Europa gebaut wurde. Die bekanntesten, von ihm entworfenen quaderförmigen Bauten stehen in der Stadt Chicago, USA.

Quader Architektenanordnung

 in Computergrafik, Verschiedenes

Mein Java-Programm Zentralperspektive habe ich benutzt, um ein quaderförmiges Gebäude in Übereck-Ansicht in der so genannten Architektenanordnung darzustellen. Im Architekturstudium lernt man, wie sich aus Grund- und Aufriss des Bauwerks dessen zentralperspektivische Ansicht konstruieren lässt. Die Konstruktionsvorschrift habe ich in mein Programm eingearbeitet. Das Programm zeichnet die Linien und markiert die Punkte,  die bei der Konstruktion wichtig sind (Horizont, Standlinie, die Spuren der Sehstrahlen, Haupt- und Augpunkt un die beiden Fluchtpunkte). Es ist nicht sehr übersichtlich geschrieben – schließlich wollte ich nur testen, ob das Ergebnis richtig ist. Das ist in der Tat der Fall, die  beiden mit dem Programm erstellten Zeichnungen sind in Ordnung. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Abbildungen: Zwei perspektive Bilder eines Quaders in Architektenanordnung (schwarze Linien), grün: Grund- und Aufriss. 

 

Literatur
Erich Hartmann: Darstellende Geometrie für Architekten, Fachbereich Mathemtik, TU-Darmstadt.
www2.mathematik.tu-Darmstadt.de/dga-incl-loes.pdf

 

Nachtrag zur Adventszeit – Herrnhuter Stern

 in Computergrafik, Verschiedenes

Beim weihnachtlichen Stöbern im Internet stoße ich auf einen Artikel von J. Böhm1, der ein Derive-Programm zum Zeichnen des Herrnhuter Sterns beschreibt. Für mich ein Anlass, dasselbe mit Maple zu versuchen, der Software, die ich als Mathematik-Programm benutze. Dieser Versuch dauerte länger als  geplant – ich hatte lange nicht mehr mit dem Maple-System gearbeitet und vieles vergessen.
Zunächst lernte ich, dass der Rumpfkörper des Sterns ein archimedischer Körper ist, also ein konvexer Vielflächner, dessen Seitenflächen regelmäßige Vielecke sind und dessen Ecken sich zueinander gleich verhalten. Der Rumpfkörper des Herrnhuter Sterns ist ein Rhombenkuboktaeder. Seine Oberfläche besteht aus 18 Quadraten und 8 gleichseitigen Dreiecken. Jeweils drei Quadrate und ein Dreieck bilden eine Raumecke, und jeweils 8 Kanten sind Kanten eines regelmäßigen Achtecks. Insgesamt gibt es sechs dieser Achtecke. Die Zacken des Sterns entstehen, indem man auf jeder Seitenfläche des Rumpfkörpers eine gerade Pyramide errichtet, insgesamt also 18 quadratische Pyramiden und 8 Pyramiden mit der Grundfläche eines gleichseitigen Dreiecks.

Zum Zeichnen der Pyramiden benötigt man die Koordinaten der Eckpunkte des Rumpfkörpers – sie bilden die 18 Quadrate und 8 Dreiecke der Pyramiden-Grundfläche – und die Koordinaten der jeweiligen Pyramidenspitze. Da der Rhombenkuboktaeder zu jeder seiner Mittelachsen drehsymmetrisch ist, genügt es, die Eckpunktkoordinaten einer Seitenfläche zu ermitteln und diese Koordinaten einer Drehung um die passende Achse zu unterwerfen. Um die Koordinaten der jeweiligen Pyramidenspitze zu erzeugen, errichten wir über dem Mittelpunkt der Seitenfläche die Flächennormale. Diese Gerade bringen wir zum Schnitt mit einer Kugel von frei wählbarem Radius. Die Abbildung zeigt die Zeichnung, das Foto einen realen Herrnhuter Stern.   Mehr zur Rechnung und zum Programmcode.

1  Josef Böhm, Der Herrnhuter Stern, nojo.boehm@pgv.at

Klever Fluchtlinien (Nachtrag)

 in Computergrafik, Verschiedenes

In den »Klever Fluchtlinien« ging es um des Test eines Computerprogramms, das (zentral-)perspektivische Darstellungen in einer Bildebene  (Leinwand oder Zeichenkarton) berechnet. Der Blick vom Obelisken auf dem Klever Springenberg in Richtung Hoch Elten war dasTestobjekt: Die Perspektive entlang dieser Sichtachse sollte vom Computerprogramm wiedergegeben werden. Das war auch der Fall: Der »vanishing point« der Fluchtlinien lag genau dort, wo er geografisch liegen sollte – wenige Meter unterhalb der Kirche St. Vitus in Hoch Elten.

Den Eltener Hügel mit der Kirche habe ich vor einigen Tagen besucht. Dort ist die Skulptur »Stein Tor« des Bildhauers Christoph Wilmsen-Wiegmann nicht zu übersehen: Zwei riesige, parallel aufgestellte Basaltpfeiler lassen einen schmalen Spalt offen, hinter dem, aus Richtung Kleve betrachtet, der Kirchturm von St. Vitus erscheint. Das also ist er – der »Fluchtpunkt«. Dazu, im Boden eingelassen, ein länglicher Steinquader, der die Richtung der Sichtachse markiert.

Die Achse ist übrigens eine grenzüberschreitende Europäerin: sie durchquert niederländisches und deutsches Gebiet. Die acht Kilometer lange Sichtstrecke ist außerdem durch eine Reihe von Skulpturen kulturell aufgeladen. 

Klever Fluchtlinien

 in Computergrafik, Verschiedenes

Vom Kriegerdenkmal auf dem Klever Springenberg sieht man bei gutem Wetter, durch eine Schneise im Wald blickend, am fernen Horizont den Kirchturm von St. Vitus in Hoch-Elten. In der Sichtlinie zur Kirche liegt im Vordergrund das von Bäumen gesäumte Wasserbecken eines Kanals, den Johann-Moritz von Nassau-Siegen seinerzeit anlegen ließ.
Schaut man etwas genauer hin, bemerkt man, dass sich die Fluchtlinien der Kanalufer und die der Baumreihen links und rechts des Wasserbeckens am Ort der Eltener Kirche treffen – eine, wie man liest, von Johann-Moritz gewollte Landschaftsgestaltung in Form einer Sichtachse. Für mich eine Gelegenheit, mein Java-Programm Zentralperspektive nochmals zu testen. Einen ersten Test hatte es schon bestanden: Der Blick in eine abschüssige und in der Ferne wieder ansteigende Straße in San Francisco wurde perspektivisch richtig wiedergegeben. Im vorliegenden Fall ist die Situation ähnlich. Das Gelände längs der Sichtlinie fällt zunächst ab, verläuft dann im Bereich des Kanals und der Rheinebene in der Horizontalen, und steigt erst nach mehreren Kilometern bis auf die Höhe des Eltener Berges wieder an.
Zum Test lasse ich das Programm die perspektivische Ansicht des Kanals und die der Baumreihen links und rechts des Kanals berechnen – und, unabhängig davon, die Lage des Bildpunktes der Eltener Kirche. Der Kanal wird durch ein langgezogenes Rechteck angenähert, mit zur Sichtlinie parallelen Längsseiten.

Das Programm benötigt als Eingabedaten die Eckpunkte des Kanal-Rechtecks und die Lage der Kirche in der realen Welt. Es verarbeitet die Daten nach den Gesetzen der Zentralperspektive und gibt die folgenden, in das nebenstehende Foto hineinkopierten geometrischen Gebilde aus: die Umrisse des Kanals (ein zum Trapez perspektivisch verkürztes Rechteck), die Linien der Baumreihen links und rechts des Kanals und die Lage des Bildpunktes der Eltener Kirche (rotes Kreuz). Die horizontale blaue Linie kennzeichnet die Höhe, in der sich der Wasserspiegel des Rheins befinden müsste. Die in das Foto zusätzlich hineinkopierten grünen Linien sind die Achsen eines Koordinatensystems, deren Schnittpunkt der Durchstoßpunkt der Sichtlinie durch die Bildebene ist (Augenpunkt). Die horizontale Achse dieses Systems ist der Horizont.

Die Längsseiten des Kanal-Rechtecks und die Linien der Baumreihen werden verlängert und treffen sich in einem gemeinsamen Fluchtpunkt. Dieser liegt, da die Linien in der realen Welt parallel zur Blickrichtung und horizontal verlaufen, im Augenpunkt auf dem Horizont. Wie zu erwarten liegt dort, zumindest in grober Näherung, auch der Bildpunkt der Eltener Kirche (rotes Kreuz). Genau genommen liegt der Bildpunkt auf der Senkrechten durch den Augenpunkt, und zwar minimal (und daher kaum erkennbar) oberhalb des Horizonts, da die Kirche in der realen Welt einige Höhenmeter mehr als der Kamera-Standort aufweist.

Das Foto zeigt im Übrigen, dass der Kamera-Standort in horizontaler Richtung nicht exakt in Kanalmitte liegt. Der Kanal wurde deshalb etwas weiter nach links verschoben (durch Änderung der X-Koordinaten seiner Eckpunkte). Berechnung und Foto stimmten danach besser überein, exakte Deckungsgleichheit ließ sich nicht herstellen. Die (kleine) Korrektur äußert sich in der seitlichen Verschiebung der vertikalen grünen Koordinatenachse gegenüber der Mitte des Kanals – und gegenüber der Statue vorne im Bild (Balkenhols »Neuer Eiserner Mann«).

Insgesamt betrachtet, gibt es zwar kleine Abweichungen zwischen Theorie und Praxis, beispielsweise zwischen dem im Foto abgebildeten und dem theoretisch berechneten Kanalufer. Aber abgesehen davon wird die reale Welt durch das Programm richtig in die Bildebene transformiert. Das Programm hat einen weiteren Test bestanden. Eine ausführlichere Beschreibung des Tests hier.

Es gibt im Übrigen in Kleve weitere Schneisen, Wege und Alleen, die auf markante Bauwerke oder Landschaftspunkte ausgerichtet sind, beispielsweise die „Galleien“ in der Ebene des Kermisdal-Bogens. Sie wurden auch von Johann-Moritz angelegt. 

Marmor an der Lahn

 in Computergrafik, Wanderlust

Eine Überraschung auf dem Lahnwanderweg: Der UNICA-Bruch bei Villmar an der Lahn. Er war, so liest man, einer der vielen Steinbrüche, in denen der Lahn-Marmor abgebaut wurde. Heute ist er in Rente und lehrt Erdgeschichte. Zwei Terrassen mit glatt gesägten Wänden bieten einen Einblick in das Leben in den Riffen des Devon-Meeres – vor 380 Millionen Jahren. Die angeschliffenen Kalk-Skelette der damaligen Meerestiere (linkes Bild) erinnern an Computergrafiken. Sie sehen aus wie Darstellungen von JULIA-Mengen mit Siegel-Disks, die mein Rechner seinerzeit ausdruckte. Ein passendes Exemplar (rechtes Bild) habe ich aus dem Archiv ausgegraben.

Spiegelungen mit Zirkel und Lineal

 in Computergrafik

Abb_6Das Problem, Spiegelungen zentralperspektivisch darzustellen, lässt mir keine Ruhe. Inzwischen bin ich zwar sicher, dass mein Computerprogramm vernünftige Ergebnisse liefert (mehr dazu hier). Aber neu ist die Erkenntnis, dass man das perspektivische Bild einer Spiegelung auch mit Zirkel und Lineal konstruieren kann. Die alten Meister wussten offenbar, wie man das macht, sie hatten noch keine Computer.  Dieses Wissen ist natürlich nicht verloren gegangen, Anleitungen für solche Konstruktionen findet man in der Literatur zur Genüge.

Damit ergibt sich die Frage: sind diese Konstruktionsanleitungen verträglich mit der Mathematik, die ich im Computerprogramm benutze? Zwei einfache Beispiele habe ich „durchgerechnet” – sie sind es. Die Skizze zeigt eine dieser Konstruktionen1: Das Spiegelbild (blau) eines Quaders (schwarz) an einem vertikalen Spiegel (rot). Das andere Beispiel ist die Spiegelung an einer Wasseroberfläche. Details zu den beiden Rechnungen hier.

1 nach Bruce MacEvoy: elements of perspective, www.handprint.com/HP/WCL/perspect6.html

Gespiegelt und zentralprojiziert

 in Computergrafik

Reinhardtsgrimma_04_mit_Foto_MMQuader_Vert_Spiegel_FotoQuader_Vert_Spiegel_Computerausdruck

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Das Bild, das ein Spiegel oder eine ebene Wasseroberfläche von einem Gegenstand erzeugt, folgt den Gesetzen der Optik: Der Lichtstrahl, der von einem Punkt des Gegenstandes ausgeht und unser Auge trifft, wird an der Spiegelebene so reflektiert, dass Einfalls- und Ausfallswinkel gleich sind. Eine einfache Sache. Schwieriger wird es, wenn Gegenstand und Spiegelbild, wie zum Beispiel in der Malerei, zentralperspektivisch darzustellen sind. Eine perspektivisch richtige Darstellung kann man berechnen. Dazu benötigt man etwas Lineare Algebra –  nur ein paar Grundkenntnisse über Matrizen und Vektoren. Sie sind ohne Schwierigkeiten in ein Computerprogramm einzubauen. Das habe ich getan. Von dem Programm will man natürlich wissen, ob es richtig rechnet. Also muss ein Test her.

Mein Computerprogramm ist einfach: Es kann nur einen einzigen geometrischen Körper spiegeln, nämlich einen Quader (ein Gebilde von der Form einer Streichholzschachtel). Gesucht war deshalb ein Foto mit einem Objekt, das sich durch einen Quader annähern lässt, und das auch noch gepiegelt wird. Das Gebäude auf dem Bild links erschien  mir als Testobjekt geeignet. Es liegt auf einer kleinen Anhöhe im Hintergrund des Bildes und spiegelt sich in einem Teich im Vordergrund. Wen es interessiert: es ist das Badehaus im Schlosspark von Reinhardtsgrimma  (Ortsteil von Glashütte in Sachsen). Mein Testobjekt wird zum Quader vereinfacht und dann dem Computerprogramm zur Verarbeitung eingegeben. Der zeichnet die Umrisse von Quader (Original) und Spiegelbild auf den Bildschirm. Ich habe sie in das Foto hineinkopiert. Die Fluchtlinien der horizontalen Quaderkanten laufen in zwei Fluchtpunkten zusammen, einer dieser Punkte ist sichtbar. Wie man sieht, hat der Computer richtig gerechnet – jedenfalls für den Fall horizontaler Spiegelebenen.

Natürlich sollte das Computerprogramm auch für andere Objekt/Spiegel-Anordnungen richtig rechnen. Die beiden Abbildungen rechts zeigen das Beispiel einer Spiegelung an einer vertikalen reflektierenden Ebene, im Alltagsleben als Wandspiegel bekannt. Oben das Foto, darunter der Computerausdruck. Der Vergleich zeigt, dass die Umrisse des Quaders recht gut berechnet werden. Das Computerprogramm liefert also auch in diesem Fall ein plausibles Ergebnis. Test bestanden. Mehr über die Mathematik der Spiegelung und das Programm hier.

Fibonacci-Rechtecke

 in Computergrafik, Verschiedenes

Fibonacci_RechteckeEine kleine Spielerei mit der bekannten Zahlenfolge:

Nimm die Folge (Fn) =  0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,… (n = 0, 1, 2 , 3 …) der Fibonacci-Zahlen1 und bilde die Produkte benachbarter Zahlen 0×1 = 0, 1×1 = 1, 1×2 = 2, 2×3 = 6, 3×5 = 15, 5×8 = 40, usw. Die Produkte 0, 1, 2, 6, 15, 40, usw. sind die Flächeninhalte der so genannten Fibonacci-Rechtecke2 mit den Seitenlängen (0,1), (1,1), (1,2), (2,3), (3,5), (5,8), ….  Addiere die ersten n Flächeninhalte. Dann entsteht die Zahlenfolge (an) =  0, 1, 3, 9, 24, 64, 168, 441, 1155, 3025, …, die Summe der Fläche der ersten n Fibonacci-Recktecke3.  In der Abbildung sind die Fibonacci-Rechtecke spiralförmig aneinander gelegt. Man erkennt sofort, dass jedes zweite Rechteck die bisher angelegten zu einem Quadrat ergänzt. Das heißt, jedes zweite Glied der Folge (an) ist eine Quadratzahl: 1 = 12, 9 = 32, 64 = 82, 441 = 212 und 3025 = 552, und zwar das Quadrat einer Fibonacci-Zahl mit geradem Index: 12 = F22, 32  = F42, 82 = F62, 212 = F82. Beweis durch vollständige Induktion.

Die Fibonacci-Rechteck-Spirale ist sicher keine Entdeckung von mir. Ich habe sie aber bisher in der Literatur noch nicht gefunden. Wen es interessiert, zwei kleine Notizen zum Thema: Fibonacci-Folge und Goldener Schnitt und Formel von Moivre/Binet. Oder wie wär’s mit einem Ausflug in die Lineare Algebra: Moivre/Binet (Beweis mit LA) .

… und da gerade das Stichwort „Fibonacci“ fällt, hier noch ein Nachtrag zur Jahreszahl 2017. Nach Zeckendorf kann jede natürliche Zahl n  > 0  eindeutig als Summe voneinander verschiedener, nicht direkt aufeinanderfolgender Fibonacci-Zahlen geschrieben werden. Die Zeckendorf-Zerlegung unserer Jahreszahl ist 2017 = 1597 + 377 + 8 + 1.

 

1     The On-Line Encyclopedia of Integer Sequences (A000045)
2     a. a. O., (A001654)
3     a. a. O., (A064831)