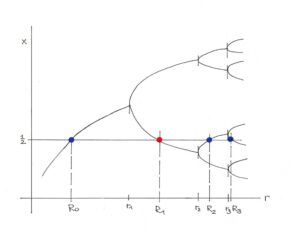
Berechnung der Feigenbaumkonstante

 in Computergrafik

Die Feigenbaumkonstante ist eine universale Konstante der mathematischen Logistik. Ihr „Entdecker“ und Namensgeber ist der US-amerikanische Physiker Mitchell Jay Feigenbaum. Es geht um das Verhalten der Iterationen xn+1 = fr(xn) der logistischen Funktion fr(xn) = rxn(1 – xn). Der Verlauf der Grenzwerte von xn+1 = fr(xn) für n→unendlich, aufgetragen in Abhängigkeit des Parameters r, heißt Bahn der logistischen Funktion. Abbildung 1 zeigt diese Bahn für 1 < r < 4. Sie zeichnet sich dadurch aus, dass sie an der Stelle r = 3 in zwei Gabelzinken aufspaltet und diese Aufspaltung (Bifurkation) sich bei höheren Werten von r mehrmals fortsetzt. Bei jeder Gabelung verdoppelt sich die Anzahl der Äste (Perioden) der Bahn und die Bifurkationsstellen rücken näher aufeinander zu. Bei etwa r = 3,56 geht die Bahn in ein Gebiet über, in dem sie viele unregelmäßige Werte annimmt. Dieses ist das Gebiet des Chaos.

 

 

 

 

 

 

 

 

 

 

 

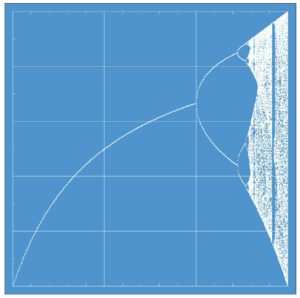
Abbildung 1: Bahn der logistischen Funktion im Intervall [1,4]. Die Bahn ist der Grenzwert der Iteration xn+1 = fr(xn) für n→unendlich. Er ist in y-Richtung aufgetragen. In x-Richtung steht als unabhängige Größe der Parameter r. Die Bahnwerte beginnen sich bei r = 3 in zwei Gabelzinken aufzuspalten. Diese Aufspaltung (Bifurkation) erfolgt danach mehrmals – bis bei etwa r = 3,56 das Chaos erreicht wird.

Die Werte ri der ersten Bifurkationsstellen sind in Tabelle 1 in Spalte 2 aufgeführt. Für i→unendlich streben sie gegen einen Grenzwert, der Feigenbaumpunkt heißt. Er liegt in etwa dort, wo das Chaos einsetzt. Die Feigenbaumkonstante δ hingegen ist der Grenzwert der Quotienten  δi = (ri+1 – ri)/(ri+2 – ri+1) für i →unendlich. Spalte 3 der Tabelle 1 zeigt die Quotienten δi für i ≤ 5. Die Zahl δ4 = 4,6686…. kommt dem Grenzwert der Feigenbaumkonstante schon recht nahe.


Tabelle 1
=============================
   i      ri          δi-1
————————————————————————————–
   1   3,0000000    –
   2   3,4494897   4,7514
   3   3,5440903   4,6562
   4   3,5644073   4,6683
   5   3,5687594   4,6686
=============================   

 

Der genaue Grenzwert δ  lässt sich nur mit einem Näherungsverfahren bestimmen – eine mathematisch aufwändige Sache. Feigenbaum war genial: er benutzte einen einfachen Taschenrechner um ihren Wert zu berechnen. Wir nehmen dazu einen Computer zur Hand.

 

 

 

 

 

 

 


Abbildung 2:  Schematische Skizze der Bahn. Die Bifurkationsstellen sind mit r1,r2,r3, … bezeichnet.
Zur Berechnung der Feigenbaumkonstanten benutzt man die Werte der superstabilen Stellen R1, R2, R3, … .

 

Das Näherungsverfahren benutzt die Tatsache, dass es zwischen zwei Bifurkationsstellen immer auch eine Stelle gibt, an denen die Iteration xn+1 = fr(xn) so genannte superstabile Fixpunkte besitzt. In Abbildung 2 sind diese Stellen mit R1,, R2, R3, … bezeichnet (die Bifurkationsstellen mit r1, r2, r3, …). Da die Werte der superstabilen Stellen zwischen jeweils zwei aufeinander folgenden Bifurkationsstellen eingeschlossen sind, haben beide Zahlenfolgen denselben Grenzwert. Zur Berechnung der Feigenbaumkonstante benutzt man die Werte der superstabilen Stellen R1,, R2, R3, … .

 

Tabelle 2
Näherungswerte für den Feigenbaumpunkt α (Spalte rN) und die Feigenbaumkonstante  δ (Spalte deltaN1).
Mit n werden die Näherungsschritte gezählt, nr ist die Anzahl der Versuche, den superstabilen Punkt zu treffen

==============================================
 n          rN          nr      deltaN1
—————————————————————————————————————————————-
  0   2,0000000000000            –
  1   3,2360679774998      4,0000000000000     
  2   3,4985616993277  6   4,7089430135405
  3   3,5546408627688  4   4,6807709980107
  4   3,5666673798563  4   4,6629596111141
  5   3,5692435316371  3   4,6684039259180
  6   3,5697952937499  3   4,6689537409485
  7   3,5699134654223  3   4,6691571814003
  8   3,5699387742333  2   4,6691910032120
  9   3,5699441946081  2   4,6691994611323
 10   3,5699453554865  2   4,6692011701107
 11   3,5699456041111  1   4,6692017591474
==============================================

 

Die Mathematik des Näherungsverfahrens – und insbesondere die Bedeutung der superstabilen Fixpunkte der Iteration xn+1 = fr(xn) – wird hier beschrieben. Das zugehörige (Java-)Computerprogramm ist nur wenige Zeilen lang. Seine numerische Genauigkeit beträgt etwa 10–14 . Mit dem Programm wurden die Näherungsschritte in Tabelle 2 berechnen. Der Literaturwert der Feigenbaumkonstante ist  δ = 4,669201609102990… . Man erkennt, dass die Näherungen bis etwa n = 10 dem Literaturwert zustreben, danach sich aber von ihm weg bewegen.

 

Literatur:
M. J. Feigenbaum, J. Stat. Phys. 19, 25 (1978).
M. J. Feigenbaum, J. Stat. Phys. 219, 665 (1978).
D. Kartofelev: Nonlinear Dynamics, Lecture Notes #11, Feigenbaum’s Analysis of Period Doubling,  
www.tud.ttu.ee/web/dmitri.kartofelev/YFX1560/LectureNotes_11.pdf.
J. H- Sylvester: Die logistische Abbildung, Das Feigenbaum-Szenario, Seminarvortrag,
www.math.uni-hamburg.de/home/lauterbach/scripts/seminar03/sylvester.
Hein-Otto Peitgen, Hartmut Jürgens und Dietmar Saupe: Fractals for the Classroom, New York, 1992,   Band 2, S. 224 ff.
N. Grzech: Die logistische Gleichung als ein Beispiel für chaotische Prozesse in der Physik, Examensarbeit, Universität Rostock,
www.wsf.uni-rostock.de/examensarbeit.pdf.

Mies van der Rohe in Krefeld

 in Computergrafik, Verschiedenes

Die bekanntesten Gebäude, die der Architekt Ludwig Mies van der Rohe entworfen hat, stehen in der Stadt Chicago (USA): das Kluczynski Federal Building, das Post Office, das 860–880 North Lake Shore Drive Building und die Crown Hall des Illinois Institutes of Technology. Sie alle sind quaderförmige Bauten, deren Fassaden sehr viel Glas enthalten. Das Glas schließt in der Regel bündig mit der Außenwand ab, so dass eine durchgehend glatte Oberfläche entsteht. Die Bauweise ist typisch für den sogenannten Internationalen Stil.

Der einzige von Mies van der Rohe entworfene Bau in Europa, der diese quaderartige Architektur aufweist, steht in Krefeld. Es ist das HE-Gebäude auf dem Gelände der ehemaligen Vereinigten Seidenwerke Krefeld (Verseidag). Da es ein perfekter Quader ist, eignet er sich gut, an ihm einige Grundaufgaben der Darstellenden Geometrie nachzuvollziehen. Das Fach »Darstellende Geometrie für Architekten« wird zwar heute noch an der Hochschule gelehrt, in der Praxis arbeitet man aber vermutlich mit der bequemeren CAD-Software.

Ich jedenfalls habe einmal spaßeshalber versucht, aus einem Foto des HE-Gebäudes (in Übereck-Ansicht) Grund- und Aufriss durch Zeichnung zu rekonstruieren. Das Ergebnis ist in Abbildung 1 zu sehen. Sie zeigt die beiden Risse in der sogenannten »Architekten-Anordnung«. Die (zeichnerische) Rekonstruktion ergibt ein Verhältnis (Länge : Breite) = 3,05, die TIM-online-Karte liefert (Länge : Breite) = 2,93 (56,47m : 19,28 m = 2,93). Das heißt, meine zeichnerische (Re-)Konstruktion kann nicht ganz falsch sein.

Abb. 1 Rekonstruktion: Grund- und Aufriss des HE-Gebäudes auf dem Gelände der ehemaligen Vereinigten Seidenwerke (Verseidag) in Krefeld. Das Gebäude ist der einzige Quaderbau, der nach dem Entwurf des Architekten Mies van der Rohe in Europa gebaut wurde. Die bekanntesten, von ihm entworfenen quaderförmigen Bauten stehen in der Stadt Chicago, USA.

Drei Aquarelle

 in Malerisches

Hohes Venn im Winter (oben),  Hohes Venn (Mitte),  Weiher im Park (unten)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Quader Architektenanordnung

 in Computergrafik, Verschiedenes

Mein Java-Programm Zentralperspektive habe ich benutzt, um ein quaderförmiges Gebäude in Übereck-Ansicht in der so genannten Architektenanordnung darzustellen. Im Architekturstudium lernt man, wie sich aus Grund- und Aufriss des Bauwerks dessen zentralperspektivische Ansicht konstruieren lässt. Die Konstruktionsvorschrift habe ich in mein Programm eingearbeitet. Das Programm zeichnet die Linien und markiert die Punkte,  die bei der Konstruktion wichtig sind (Horizont, Standlinie, die Spuren der Sehstrahlen, Haupt- und Augpunkt un die beiden Fluchtpunkte). Es ist nicht sehr übersichtlich geschrieben – schließlich wollte ich nur testen, ob das Ergebnis richtig ist. Das ist in der Tat der Fall, die  beiden mit dem Programm erstellten Zeichnungen sind in Ordnung. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Abbildungen: Zwei perspektive Bilder eines Quaders in Architektenanordnung (schwarze Linien), grün: Grund- und Aufriss. 

 

Literatur
Erich Hartmann: Darstellende Geometrie für Architekten, Fachbereich Mathemtik, TU-Darmstadt.
www2.mathematik.tu-Darmstadt.de/dga-incl-loes.pdf

 

Nachtrag zur Adventszeit – Herrnhuter Stern

 in Computergrafik, Verschiedenes

Beim weihnachtlichen Stöbern im Internet stoße ich auf einen Artikel von J. Böhm1, der ein Derive-Programm zum Zeichnen des Herrnhuter Sterns beschreibt. Für mich ein Anlass, dasselbe mit Maple zu versuchen, der Software, die ich als Mathematik-Programm benutze. Dieser Versuch dauerte länger als  geplant – ich hatte lange nicht mehr mit dem Maple-System gearbeitet und vieles vergessen.
Zunächst lernte ich, dass der Rumpfkörper des Sterns ein archimedischer Körper ist, also ein konvexer Vielflächner, dessen Seitenflächen regelmäßige Vielecke sind und dessen Ecken sich zueinander gleich verhalten. Der Rumpfkörper des Herrnhuter Sterns ist ein Rhombenkuboktaeder. Seine Oberfläche besteht aus 18 Quadraten und 8 gleichseitigen Dreiecken. Jeweils drei Quadrate und ein Dreieck bilden eine Raumecke, und jeweils 8 Kanten sind Kanten eines regelmäßigen Achtecks. Insgesamt gibt es sechs dieser Achtecke. Die Zacken des Sterns entstehen, indem man auf jeder Seitenfläche des Rumpfkörpers eine gerade Pyramide errichtet, insgesamt also 18 quadratische Pyramiden und 8 Pyramiden mit der Grundfläche eines gleichseitigen Dreiecks.

Zum Zeichnen der Pyramiden benötigt man die Koordinaten der Eckpunkte des Rumpfkörpers – sie bilden die 18 Quadrate und 8 Dreiecke der Pyramiden-Grundfläche – und die Koordinaten der jeweiligen Pyramidenspitze. Da der Rhombenkuboktaeder zu jeder seiner Mittelachsen drehsymmetrisch ist, genügt es, die Eckpunktkoordinaten einer Seitenfläche zu ermitteln und diese Koordinaten einer Drehung um die passende Achse zu unterwerfen. Um die Koordinaten der jeweiligen Pyramidenspitze zu erzeugen, errichten wir über dem Mittelpunkt der Seitenfläche die Flächennormale. Diese Gerade bringen wir zum Schnitt mit einer Kugel von frei wählbarem Radius. Die Abbildung zeigt die Zeichnung, das Foto einen realen Herrnhuter Stern.   Mehr zur Rechnung und zum Programmcode.

1  Josef Böhm, Der Herrnhuter Stern, nojo.boehm@pgv.at

Loop-Antenne für ELF-Signale

 in Physik als Hobby

Es ging um den Nachweis elektromagnetischer Wellen sehr niedriger Frequenz (engl. ELF: Extremly Low Frequency) mit einer magnetischen Antenne, in meinem Fall um den Nachweis der Schumann-Resonanzen bei 8, 16, 21, … Hz  –  bisher leider ohne Erfolg. Trotzdem einige Bemerkungen dazu:

Magnetische Antennen arbeiten nach dem Faradayschen Induktionsgesetz: Sie bestehen aus einer Leiterschleife (daher »Loop«-Antenne), in der das sich zeitlich ändernde Magnetfeld der Welle eine Spannung induziert. Die Spannung folgt dem Takt der Feldstärke des Magnetfeldes. Meine Antenne besteht aus Kupferdraht, der 600 Mal um einen quadratischen Holzrahmen mit der Seitenlänge ein Meter gewickelt ist (Abbildung 1). Das sind 600 hintereinander geschaltete Leiterschleifen, deren Spannungen sich addieren.

Abbildung 1   Foto der Antenne. Der Holzrahmen
hat eine Seitenlänge  vom 1 m. An seiner
Außenseite ist der Kabelkanal (in grauer Farbe)
zu erkennen, in dem die 600 Windungen des 
Antennendrahts untergebracht sind.

 

Das Signal aus der Summe der Spannungen wird mit Hilfe einer schnellen Fourier-Transformation (FFT) nach Frequenzen sortiert und als »Spektrum« auf dem Bildschirm eines PC dargestellt. In dieser Darstellung sollten sich die Schumann-Resonanzen als etwa 4 Hz breite Buckel (»Peaks«) zeigen. Das ist leider nicht der Fall (Abbildung 2). Es sind Linien bei 16,7 Hz, 33,3 Hz (Bahnstrom und Oberwelle) und 50 Hz (Energie-Versorgungsnetz) deutlich sichtbar, aber keine Peaks bei 8, 16 und 21 Hz –  das heißt, keine Schumann-Resonanzen. Offenbar war bei meinen Messungen (in unmittelbarer Nähe des Hauses) der Pegel des Umgebungsrauschens zu hoch, um die Schumann-Signale aus diesem Rauschen herauszufiltern.

 

Abbildung 2  Spektrum des Antennenrauschens meiner Loop
für Frequenzen unterhalb 50 Hz. Es sind Linien bei 16,7 Hz, 33,3 Hz
(Bahnstrom und Oberwelle) und 50 Hz (Energie-Versorgungsnetz)
deutlich sichtbar, aber keine Schumann-Resonanzen.

 

 

Dass die Antenne bei ausreichend starken Signalen richtig arbeitet, zeigt ein Ausschnitt des Spektrums bei höheren Frequenzen: Das Signal des Zeitzeichen-Senders DCF77 bei 77,5 kHz wird deutlich empfangen (Abbildung 3). 

 

 

Abbildung 3  Ausschnitt aus dem Empfangsspektrum der Loop
für Frequenzen im Bereich Kilohertz. Die Linie bei 77,5 kHz
ist das Signal des Zeitzeichen-Senders DCF77.

 

Obwohl ich keine Schumann-Resonanzen nachzuweisen konnte, hier einige Überlegungen zur Theorie der magnetischen Antenne und deren Konstruktion.

Auf dem Weg ins Chaos

 in Physik als Hobby

Das Chaos  – gemeint ist das Chaos in der Physik – hat mich schon vor Jahren fasziniert: Ein Eintrag in meinem Protokollbuch aus dem Jahr 1993 (Abbildung 1) zeigt einen  elektromagnetischen Schwingkreis, der eine Diode als nichtlineares Element enthält. An dem wollte ich die Periodenverdopplung studieren, die dem Chaos vorausgeht. Offenbar ohne Erfolg, denn weitere Einträge fehlen. Das seltsame Verhalten nichtlinearer Schwingungen, die Periodenverdopplung,  hatte der US-amerikanische Physiker Mitchell J. Feigenbaum¹ vorhergesagt.

Abbildung 1   Vor 30 Jahren schon einmal versucht, zum Chaos
vorzudringen (ohne Erfolg): Eintrag ins Protokollbuch vom 15.08.1993.

 

 

Jetzt ein neuer Versuch – Versuch im wahrsten Sinn des Wortes. Mein Schwingkreis bestand dieses Mal aus einem 100 Ohm-Widerstand , einer Spule mit der Induktivität 8,2 mH und der Diode 1N4007, betrieben bei der Frequenz 100 kHz. Den Weg zum Chaos beschreitet man, indem man die am Kreis anliegende Spannung U fortlaufend erhöht. Das tat ich – in kleinen Schritten – und beobachtete dabei die Spannung über der Diode. Ihre Periode verdoppelte sich tatsächlich mehrmals, wie von Feigenbaum vorhergesagt (untere Oszillogramme in den Abbildungen 2).

Die Spannungsschwellen US für Periodenverdopplung lieferten auch einen sinnvollen Wert für den ersten Feigenbaum-Quotienten, nämlich δ1 = 4,62 ± 1,14. (δ ist das Verhältnis der Differenzen zwischen den Spannungsschwellen zweier aufeinanderfolgender Periodenverdopplungen). Mehr zum Experiment.

1  M. J. Feigenbaum, J. Stat. Phys. 19, 25 (1978), und M. J. Feigenbaum, J. Stat. Phys. 21, 665 (1978).

 

 

 

Abbildung 2   Periodenverdopplung der Spannung über der Diode (jeweils unteres Oszillogramm): a) eine Periode, b) zwei Perioden, c) vier Perioden.

»Spectroscopy of Light Nuclei…« – Kernphysik vor fünfzig Jahren

 in Physik als Hobby, Verschiedenes

In meinem ersten Beruf war ich Physiker und in der Forschung tätig. Ich arbeitete in einer Gruppe von Wissenschaftlern am Institut für Kernphysik der Technischen Hochschule (heute »Technische Universität«) Darmstadt. Unser Forschungsgebiet war die Streuung von Elektronen an Atomkernen. Die Elektronen lieferte der Elektronen-Linearbeschleuniger (»Dalinac«) des Instituts. Ein ehemaliger Teamkollege erinnerte mich kürzlich an einen wissenschaftlichen Artikel¹, den ich seinerzeit geschrieben hatte – vor genau fünfzig Jahren. Er zitiert ihn in einer seiner eigenen Arbeiten². Mein Artikel war ein Review, das heißt, eine Zusammenfassung von damals vorliegenden Forschungsergebnissen. Die meisten stammten aus dem Darmstädter Institut.  Angeleitet und wissenschaftlich betreut wurden wir vom Direktor des Instituts, Professor Peter Brix. 

Prof. Dr. Peter Brix

Ich habe der Forschung den Rücken gekehrt, mein Kollege ist ihr treu geblieben. Er lehrt heute an der Universität Mainz und betreibt weiterhin Elektronenstreuung – mit wesentlich modernerem Equipment als damals. Peter Brix, unser akademischer Lehrer verbindet uns. Ich verdanke ihm meine Begeisterung für Physik, auch wenn ich sie  später auf niedrigerem als Hochschulniveau betrieben habe. Er sollte deshalb nicht in Vergessenheit geraten: Das Foto zeigt Peter Brix bei einem Vortrag über Elektronenstreuung – beachte seinen makellosen Tafelanschrieb.

Ich persönlich erinnere mich mit Dankbarkeit an die Zeit in Darmstadt. Die Arbeit am Institut für Kernphysik gehört zu den angenehmsten beruflichen Erfahrungen, auf die ich zurückblicke – sowohl in wissenschaftlicher als auch menschlicher Hinsicht.

1 H. Theissen: »Spectroscopy of Light Nuclei by Low Energy (< 70 MeV) Inelastic Electron Scattering«, Springer Tracs in Modern Physics, Vol. 65 (1972)

2  S. Kegel et al.: »Measurement of the α-particle monopole transition form factor challenges theory: a low-energy puzzle for nuclear forces?«. Wann und in welcher Fachzeitschrift der Artikel erschienen ist, weiß ich nicht. Der ehemalige Teamkollege, jetzt an der Universität Mainz, ist Professor Th. Walcher, einer der Autoren dieses Artikels