 Eine kleine Spielerei mit der bekannten Zahlenfolge:
Eine kleine Spielerei mit der bekannten Zahlenfolge:
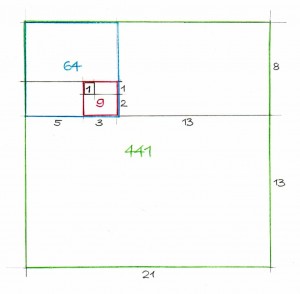
Nimm die Folge (Fn) = 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,… (n = 0, 1, 2 , 3 …) der Fibonacci-Zahlen1 und bilde die Produkte benachbarter Zahlen 0×1 = 0, 1×1 = 1, 1×2 = 2, 2×3 = 6, 3×5 = 15, 5×8 = 40, usw. Die Produkte 0, 1, 2, 6, 15, 40, usw. sind die Flächeninhalte der so genannten Fibonacci-Rechtecke2 mit den Seitenlängen (0,1), (1,1), (1,2), (2,3), (3,5), (5,8), …. Addiere die ersten n Flächeninhalte. Dann entsteht die Zahlenfolge (an) = 0, 1, 3, 9, 24, 64, 168, 441, 1155, 3025, …, die Summe der Fläche der ersten n Fibonacci-Recktecke3. In der Abbildung sind die Fibonacci-Rechtecke spiralförmig aneinander gelegt. Man erkennt sofort, dass jedes zweite Rechteck die bisher angelegten zu einem Quadrat ergänzt. Das heißt, jedes zweite Glied der Folge (an) ist eine Quadratzahl: 1 = 12, 9 = 32, 64 = 82, 441 = 212 und 3025 = 552, und zwar das Quadrat einer Fibonacci-Zahl mit geradem Index: 12 = F22, 32 = F42, 82 = F62, 212 = F82. Beweis durch vollständige Induktion.
Die Fibonacci-Rechteck-Spirale ist sicher keine Entdeckung von mir. Ich habe sie aber bisher in der Literatur noch nicht gefunden. Wen es interessiert, zwei kleine Notizen zum Thema: Fibonacci-Folge und Goldener Schnitt und Formel von Moivre/Binet. Oder wie wär’s mit einem Ausflug in die Lineare Algebra: Moivre/Binet (Beweis mit LA) .
… und da gerade das Stichwort „Fibonacci“ fällt, hier noch ein Nachtrag zur Jahreszahl 2017. Nach Zeckendorf kann jede natürliche Zahl n > 0 eindeutig als Summe voneinander verschiedener, nicht direkt aufeinanderfolgender Fibonacci-Zahlen geschrieben werden. Die Zeckendorf-Zerlegung unserer Jahreszahl ist 2017 = 1597 + 377 + 8 + 1.
1 The On-Line Encyclopedia of Integer Sequences (A000045)
2 a. a. O., (A001654)
3 a. a. O., (A064831)
