Eine interessante Anwendung der Theorie gekoppelter Schwingungen wurde vor etwa 70 Jahren von E. U. Condon (in Zusammenarbeit mit P.E. Condon) vorgestellt1 – das Problem geht offenbar zurück auf eine noch ältere Arbeit von Lord Kelvin2. Es ging um die Frage, in welcher Weise der Gang einer Taschenuhr durch (Dreh-)Schwingungen ihres Gehäuses beeinflusst wird. Ein entsprechendes Experiment sollte darüber Aufschluss geben.
Das Ergebnis war, dass der Gang der Uhr in der Tat durch die Kopplung zwischen dem „Schwungrad“ des Uhrwerks (dem Unruh-Ring) und dem Gehäuse beeinflusst wird. Diese Kopplung wird durch die Spiralfeder hergestellt, die das Rückstellmoment für den Unruh-Ring liefert. Es gibt also Abweichungen im Gang der Uhr von der Zeit, die gemessen wird, wenn das Gehäuse gegen Drehung fixiert ist. Und zwar so, dass die Uhr schneller geht, wenn die Eigenfrequenz des Gehäuses kleiner ist als die der Unruh, und dass sie langsamer geht, wenn die Gehäuse-Eigenfrequenz größer als die der Unruh ist.
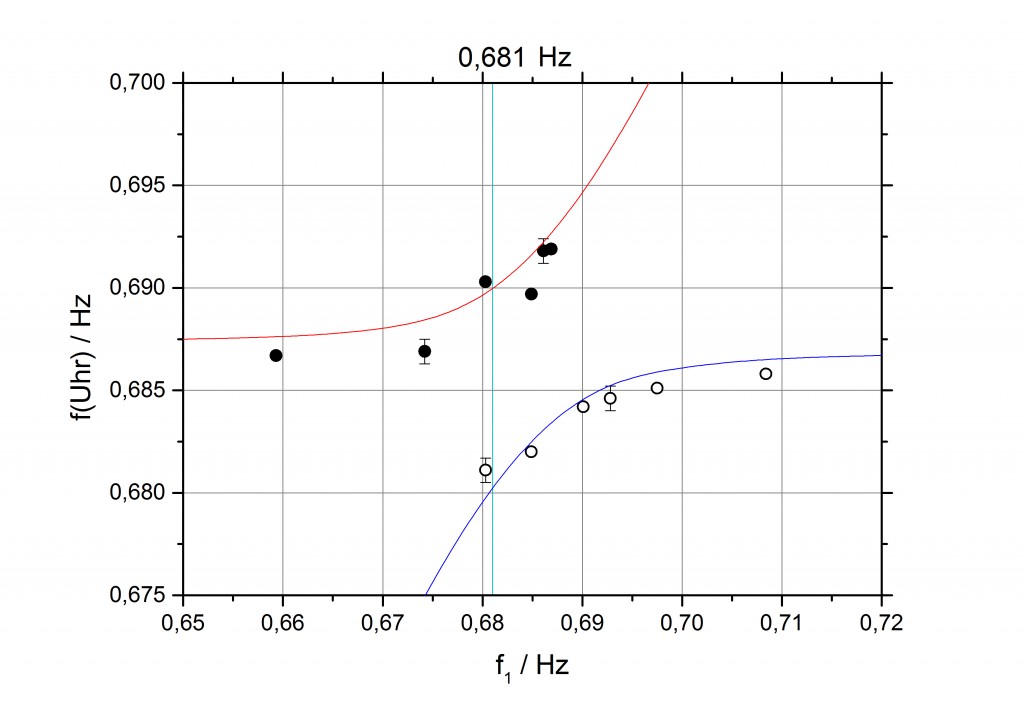
Das Condon’sche Uhrenexperiment faszinierte mich, als ich vor Jahren zum ersten Mal davon erfuhr. Jetzt, nach langer Zeit, ein bescheidener Versuch, die Physik des Experiments nachzuvollziehen – soweit das mit einfachen Mitteln möglich ist. Die Idee: ein Modell-Experiment mit zwei durch eine Spiralfeder gekoppelten Fadenpendeln. Keine Simulation, die wäre wegen des großen Massenunterschieds zwischen Gehäuse und Uhrwerk-Unruh zu aufwändig gewesen. Die eigenen Versuche dazu waren trotzdem interessant. In der Abbildung sind die Frequenzen f der Normalschwingungen zweier gekoppelter Fadenpendel aufgetragen, von denen eines das „Uhren“-Pendel, das andere das „Gehäuse“-Pendel darstellte. Sie sind aufgetragen als Funktion der Eigenfrequenz f1 des „Gehäuse“-Pendels.
1 E. U. Condon und P. E. Condon: Effect of Oscillations of the Case on the Rate of a Watch, A. J. Phys. 16, 14 – 16 (1948)
2 Lord Kelvin: Popular lectures and addresses, MacMillan 1894
