Das Chaos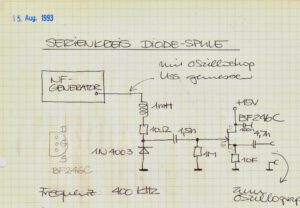
– gemeint ist das Chaos in der Physik – hat mich schon vor Jahren fasziniert: Ein Eintrag in meinem Protokollbuch aus dem Jahr 1993 (Abbildung 1) zeigt einen elektromagnetischen Schwingkreis, der eine Diode als nichtlineares Element enthält. An dem wollte ich die Periodenverdopplung studieren, die dem Chaos vorausgeht. Offenbar ohne Erfolg, denn weitere Einträge fehlen. Das seltsame Verhalten nichtlinearer Schwingungen, die Periodenverdopplung, hatte der US-amerikanische Physiker Mitchell J. Feigenbaum¹ vorhergesagt.
Abbildung 1 Vor 30 Jahren schon einmal versucht, zum Chaos
vorzudringen (ohne Erfolg): Eintrag ins Protokollbuch vom 15.08.1993.
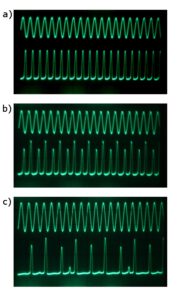Jetzt ein neuer Versuch – Versuch im wahrsten Sinn des Wortes. Mein Schwingkreis bestand dieses Mal aus einem 100 Ohm-Widerstand , einer Spule mit der Induktivität 8,2 mH und der Diode 1N4007, betrieben bei der Frequenz 100 kHz. Den Weg zum Chaos beschreitet man, indem man die am Kreis anliegende Spannung U fortlaufend erhöht. Das tat ich – in kleinen Schritten – und beobachtete dabei die Spannung über der Diode. Ihre Periode verdoppelte sich tatsächlich mehrmals, wie von Feigenbaum vorhergesagt (untere Oszillogramme in den Abbildungen 2).
Die Spannungsschwellen US für Periodenverdopplung lieferten auch einen sinnvollen Wert für den ersten Feigenbaum-Quotienten, nämlich δ1 = 4,62 ± 1,14. (δ ist das Verhältnis der Differenzen zwischen den Spannungsschwellen zweier aufeinanderfolgender Periodenverdopplungen). Mehr zum Experiment.
1 M. J. Feigenbaum, J. Stat. Phys. 19, 25 (1978), und M. J. Feigenbaum, J. Stat. Phys. 21, 665 (1978).
Abbildung 2 Periodenverdopplung der Spannung über der Diode (jeweils unteres Oszillogramm): a) eine Periode, b) zwei Perioden, c) vier Perioden.