Mies van der Rohe in Krefeld

 in Verschiedenes

Die bekanntesten Gebäude, die der Architekt Ludwig Mies van der Rohe entworfen hat, stehen in der Stadt Chicago (USA): das Kluczynski Federal Building, das Post Office, das 860–880 North Lake Shore Drive Building und die Crown Hall des Illinois Institutes of Technology. Sie alle sind quaderförmige Bauten, deren Fassaden sehr viel Glas enthalten. Das Glas schließt in der Regel bündig mit der Außenwand ab, so dass eine durchgehend glatte Oberfläche entsteht. Die Bauweise ist typisch für den sogenannten Internationalen Stil.

Der einzige von Mies van der Rohe entworfene Bau in Europa, der diese quaderartige Architektur aufweist, steht in Krefeld. Es ist das HE-Gebäude auf dem Gelände der ehemaligen Vereinigten Seidenwerke Krefeld (Verseidag). Da es ein perfekter Quader ist, eignet er sich gut, an ihm einige Grundaufgaben der Darstellenden Geometrie nachzuvollziehen. Das Fach »Darstellende Geometrie für Architekten« wird zwar heute noch an der Hochschule gelehrt, in der Praxis arbeitet man aber vermutlich mit der bequemeren CAD-Software.
Ich jedenfalls habe einmal spaßeshalber versucht, aus einem Foto des HE-Gebäudes (in Übereck-Ansicht) Grund- und Aufriss durch Zeichnung zu rekonstruieren. Das Ergebnis ist in Abbildung 1 zu sehen. Sie zeigt die beiden Risse in der sogenannten »Architekten-Anordnung«. Die (zeichnerische) Rekonstruktion ergibt ein Verhältnis (Länge : Breite) = 3,05, die TIM-online-Karte liefert (Länge : Breite) = 2,93 (56,47m : 19,28 m = 2,93). Das heißt, meine zeichnerische (Re-)Konstruktion kann nicht ganz falsch sein.

Abb. 1 Rekonstruktion: Grund- und Aufriss des HE-Gebäudes auf dem ehemaligen Gelände der Vereinigten Seidenwerke (Verseidag) in Krefeld.

Nachtrag zur Adventszeit – Herrnhuter Stern

 in Computergrafik, Verschiedenes

Beim weihnachtlichen Stöbern im Internet stoße ich auf einen Artikel von J. Böhm1, der ein Derive-Programm zum Zeichnen des Herrnhuter Sterns beschreibt. Für mich ein Anlass, dasselbe mit Maple zu versuchen, der Software, die ich als Mathematik-Programm benutze. Dieser Versuch dauerte länger als  geplant – ich hatte lange nicht mehr mit dem Maple-System gearbeitet und vieles vergessen.
Zunächst lernte ich, dass der Rumpfkörper des Sterns ein archimedischer Körper ist, also ein konvexer Vielflächner, dessen Seitenflächen regelmäßige Vielecke sind und dessen Ecken sich zueinander gleich verhalten. Der Rumpfkörper des Herrnhuter Sterns ist ein Rhombenkuboktaeder. Seine Oberfläche besteht aus 18 Quadraten und 8 gleichseitigen Dreiecken. Jeweils drei Quadrate und ein Dreieck bilden eine Raumecke, und jeweils 8 Kanten sind Kanten eines regelmäßigen Achtecks. Insgesamt gibt es sechs dieser Achtecke. Die Zacken des Sterns entstehen, indem man auf jeder Seitenfläche des Rumpfkörpers eine gerade Pyramide errichtet, insgesamt also 18 quadratische Pyramiden und 8 Pyramiden mit der Grundfläche eines gleichseitigen Dreiecks.

Zum Zeichnen der Pyramiden benötigt man die Koordinaten der Eckpunkte des Rumpfkörpers – sie bilden die 18 Quadrate und 8 Dreiecke der Pyramiden-Grundfläche – und die Koordinaten der jeweiligen Pyramidenspitze. Da der Rhombenkuboktaeder zu jeder seiner Mittelachsen drehsymmetrisch ist, genügt es, die Eckpunktkoordinaten einer Seitenfläche zu ermitteln und diese Koordinaten einer Drehung um die passende Achse zu unterwerfen. Um die Koordinaten der jeweiligen Pyramidenspitze zu erzeugen, errichten wir über dem Mittelpunkt der Seitenfläche die Flächennormale. Diese Gerade bringen wir zum Schnitt mit einer Kugel von frei wählbarem Radius. Die Abbildung zeigt die Zeichnung, das Foto einen realen Herrnhuter Stern.   Mehr zur Rechnung und zum Programmcode.

1  Josef Böhm, Der Herrnhuter Stern, nojo.boehm@pgv.at

Loop-Antenne für ELF-Signale

 in Physik als Hobby

Es ging um den Nachweis elektromagnetischer Wellen sehr niedriger Frequenz (engl. ELF: Extremly Low Frequency) mit einer magnetischen Antenne, in meinem Fall um den Nachweis der Schumann-Resonanzen bei 8, 16, 21, … Hz  –  bisher leider ohne Erfolg. Trotzdem einige Bemerkungen dazu:

Magnetische Antennen arbeiten nach dem Faradayschen Induktionsgesetz: Sie bestehen aus einer Leiterschleife (daher »Loop«-Antenne), in der das sich zeitlich ändernde Magnetfeld der Welle eine Spannung induziert. Die Spannung folgt dem Takt der Feldstärke des Magnetfeldes. Meine Antenne besteht aus Kupferdraht, der 600 Mal um einen quadratischen Holzrahmen mit der Seitenlänge ein Meter gewickelt ist (Abbildung 1). Das sind 600 hintereinander geschaltete Leiterschleifen, deren Spannungen sich addieren.

Abbildung 1   Foto der Antenne. Der Holzrahmen
hat eine Seitenlänge  vom 1 m. An seiner
Außenseite ist der Kabelkanal (in grauer Farbe)
zu erkennen, in dem die 600 Windungen des 
Antennendrahts untergebracht sind.

 

Das Signal aus der Summe der Spannungen wird mit Hilfe einer schnellen Fourier-Transformation (FFT) nach Frequenzen sortiert und als »Spektrum« auf dem Bildschirm eines PC dargestellt. In dieser Darstellung sollten sich die Schumann-Resonanzen als etwa 4 Hz breite Buckel (»Peaks«) zeigen. Das ist leider nicht der Fall (Abbildung 2). Es sind Linien bei 16,7 Hz, 33,3 Hz (Bahnstrom und Oberwelle) und 50 Hz (Energie-Versorgungsnetz) deutlich sichtbar, aber keine Peaks bei 8, 16 und 21 Hz –  das heißt, keine Schumann-Resonanzen. Offenbar war bei meinen Messungen (in unmittelbarer Nähe des Hauses) der Pegel des Umgebungsrauschens zu hoch, um die Schumann-Signale aus diesem Rauschen herauszufiltern.

 

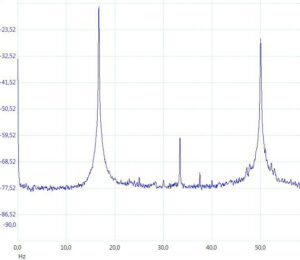Abbildung 2  Spektrum des Antennenrauschens meiner Loop
für Frequenzen unterhalb 50 Hz. Es sind Linien bei 16,7 Hz, 33,3 Hz
(Bahnstrom und Oberwelle) und 50 Hz (Energie-Versorgungsnetz)
deutlich sichtbar, aber keine Schumann-Resonanzen.

 

 

Dass die Antenne bei ausreichend starken Signalen richtig arbeitet, zeigt ein Ausschnitt des Spektrums bei höheren Frequenzen: Das Signal des Zeitzeichen-Senders DCF77 bei 77,5 kHz wird deutlich empfangen (Abbildung 3). 

 

 

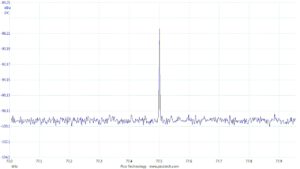Abbildung 3  Ausschnitt aus dem Empfangsspektrum der Loop
für Frequenzen im Bereich Kilohertz. Die Linie bei 77,5 kHz
ist das Signal des Zeitzeichen-Senders DCF77.

 

Obwohl ich keine Schumann-Resonanzen nachzuweisen konnte, hier einige Überlegungen zur Theorie der magnetischen Antenne und deren Konstruktion.

Auf dem Weg ins Chaos

 in Physik als Hobby

Das Chaos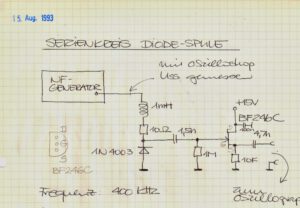  – gemeint ist das Chaos in der Physik – hat mich schon vor Jahren fasziniert: Ein Eintrag in meinem Protokollbuch aus dem Jahr 1993 (Abbildung 1) zeigt einen  elektromagnetischen Schwingkreis, der eine Diode als nichtlineares Element enthält. An dem wollte ich die Periodenverdopplung studieren, die dem Chaos vorausgeht. Offenbar ohne Erfolg, denn weitere Einträge fehlen. Das seltsame Verhalten nichtlinearer Schwingungen, die Periodenverdopplung,  hatte der US-amerikanische Physiker Mitchell J. Feigenbaum¹ vorhergesagt.

Abbildung 1   Vor 30 Jahren schon einmal versucht, zum Chaos
vorzudringen (ohne Erfolg): Eintrag ins Protokollbuch vom 15.08.1993.

 

 

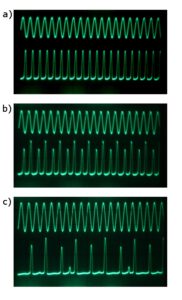Jetzt ein neuer Versuch – Versuch im wahrsten Sinn des Wortes. Mein Schwingkreis bestand dieses Mal aus einem 100 Ohm-Widerstand , einer Spule mit der Induktivität 8,2 mH und der Diode 1N4007, betrieben bei der Frequenz 100 kHz. Den Weg zum Chaos beschreitet man, indem man die am Kreis anliegende Spannung U fortlaufend erhöht. Das tat ich – in kleinen Schritten – und beobachtete dabei die Spannung über der Diode. Ihre Periode verdoppelte sich tatsächlich mehrmals, wie von Feigenbaum vorhergesagt (untere Oszillogramme in den Abbildungen 2).

Die Spannungsschwellen US für Periodenverdopplung lieferten auch einen sinnvollen Wert für den ersten Feigenbaum-Quotienten, nämlich δ1 = 4,62 ± 1,14. (δ ist das Verhältnis der Differenzen zwischen den Spannungsschwellen zweier aufeinanderfolgender Periodenverdopplungen). Mehr zum Experiment.

1  M. J. Feigenbaum, J. Stat. Phys. 19, 25 (1978), und M. J. Feigenbaum, J. Stat. Phys. 21, 665 (1978).

 

 

 

Abbildung 2   Periodenverdopplung der Spannung über der Diode (jeweils unteres Oszillogramm): a) eine Periode, b) zwei Perioden, c) vier Perioden.

»Spectroscopy of Light Nuclei…« – Kernphysik vor fünfzig Jahren

 in Physik als Hobby, Verschiedenes

In meinem ersten Beruf war ich Physiker und in der Forschung tätig. Ich arbeitete in einer Gruppe von Wissenschaftlern am Institut für Kernphysik der Technischen Hochschule (heute »Technische Universität«) Darmstadt. Unser Forschungsgebiet war die Streuung von Elektronen an Atomkernen. Die Elektronen lieferte der Elektronen-Linearbeschleuniger (»Dalinac«) des Instituts. Ein ehemaliger Teamkollege erinnerte mich kürzlich an einen wissenschaftlichen Artikel¹, den ich seinerzeit geschrieben hatte – vor genau fünfzig Jahren. Er zitiert ihn in einer seiner eigenen Arbeiten². Mein Artikel war ein Review, das heißt, eine Zusammenfassung von damals vorliegenden Forschungsergebnissen. Die meisten stammten aus dem Darmstädter Institut.  Angeleitet und wissenschaftlich betreut wurden wir vom Direktor des Instituts, Professor Peter Brix. 

Prof. Dr. Peter Brix

Ich habe der Forschung den Rücken gekehrt, mein Kollege ist ihr treu geblieben. Er lehrt heute an der Universität Mainz und betreibt weiterhin Elektronenstreuung – mit wesentlich modernerem Equipment als damals. Peter Brix, unser akademischer Lehrer verbindet uns. Ich verdanke ihm meine Begeisterung für Physik, auch wenn ich sie  später auf niedrigerem als Hochschulniveau betrieben habe. Er sollte deshalb nicht in Vergessenheit geraten: Das Foto zeigt Peter Brix bei einem Vortrag über Elektronenstreuung – beachte seinen makellosen Tafelanschrieb.

Ich persönlich erinnere mich mit Dankbarkeit an die Zeit in Darmstadt. Die Arbeit am Institut für Kernphysik gehört zu den angenehmsten beruflichen Erfahrungen, auf die ich zurückblicke – sowohl in wissenschaftlicher als auch menschlicher Hinsicht.

1 H. Theissen: »Spectroscopy of Light Nuclei by Low Energy (< 70 MeV) Inelastic Electron Scattering«, Springer Tracs in Modern Physics, Vol. 65 (1972)

2  S. Kegel et al.: »Measurement of the α-particle monopole transition form factor challenges theory: a low-energy puzzle for nuclear forces?«. Wann und in welcher Fachzeitschrift der Artikel erschienen ist, weiß ich nicht. Der ehemalige Teamkollege, jetzt an der Universität Mainz, ist Professor Th. Walcher, einer der Autoren dieses Artikels

Helmholtz-Resonator

 in Physik als Hobby

Was haben eine Flasche und eine Geige gemeinsam? Antwort: es sind beides Helmholtz-Resonatoren und damit physikalisch interessante Geräte. Sie erzeugen oder verstärken Schallschwingungen. Bei der Flasche schwingt die Luft im Flaschenhals. Den Ton erzeugen wir, indem wir seitlich über die Öffnung blasen. Bei der Geige gerät die Luft im Bereich der f-Löcher durch die Saitenschwingung in Bewegung. Das führt, vor allem bei den tiefen Geigentönen, zur Verstärkung des abgestrahlten Schalls. In beiden Fällen spielt Luft die entscheidende Rolle. Die physikalische Erklärung dazu lieferte als erster der Physiker Hermann von Helmholtz. Als Resonator bezeichnet man ein Gerät, das man zum Schwingen bringt, wenn man es mit der »richtigen« Frequenz (der »Resonanzfrequenz«) anregt.

Ein Helmholtz-Resonator besteht aus einem Hohlraum mit starren Wänden, der eine kleine Röhre als Öffnung besitzt. Schall entsteht, wenn Luft in Schwingung versetzt wird und die so erzeugten Dichteschwankungen sich ausbreiten. In unserem Fall schwingt die Luft in der Röhre des Resonators. Man kann sie als Masse auffassen, die an eine Feder gekoppelt ist. Als Feder wirkt die Luft im Hohlraum des Resonators. Sie ist eine Art Polster, erzeugt bei Kompression einen Druck und bei Expansion einen Sog, dem die Luft in der Röhre ausgesetzt ist. Dadurch wird diese hin und her bewegt. Über eigene Versuche mit Flasche und Geige hier ein ausführlicher Bericht.