Verschiedene Grautöne, mit Photosoftware erzeugt. Blick vom Kahlen Asten auf das winterliche Sauerland.
Kategorie: Verschiedenes
2020 – das Jahr mit dem Pfiff
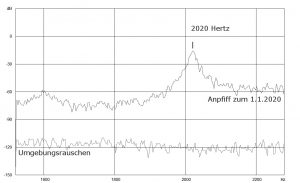
Eine etwas skurrile Performance: Wir beginnen das neue Jahr mit einem mit den Lippen erzeugten Pfeifton der Tonhöhe (Frequenz) von genau 2020 Hertz (typischer Einfall eines Physikers). In meinem PC ist, wie üblich, ein Mikrofon eingebaut, dessen Signal in einer Soundkarte digitalisiert wird. Das digitalisierte Signal wird nach der Tonhöhe sortiert (Fourier-analysiert) und das Spektrum der Tonhöhen auf dem Bildschirm dargestellt. In dieser Anordnung lässt sich die Frequenz des Pfeiftons messen. Ich beobachte also, während ich drauflos pfeife, das Tonhöhengebirge auf dem Computer-Bildschirm. Änderungen in der Lage von Zunge und Unterkiefer ergeben verschiedene Tonhöhen. Nach etwas Übung zeigt sich tatsächlich ein Matterhorn-ähnlicher Peak bei 2020 Hertz: Treffer (Abbildung oben). – Ein kleiner Mangel: Das Matterhorn dürfte etwas schroffer sein. Physiker bevorzugen Peaks mit steileren Flanken. Peaks mit Flanken in Eiger-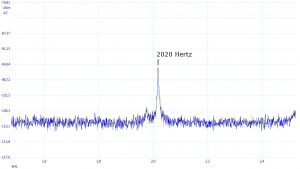 Nordwand-Qualität bedeuten, dass der Ton sehr rein ist. Auch damit kann ich dienen – allerdings mit einer anderen Art der Tonerzeugung: Der Deckel meiner Edelstahl-Teekanne sieht in etwa aus wie eine Glocke und klingt auch so. Beim Anschlag mit dem (Tee-)Löffel schwingt er mit einer ganzen Reihe von gut definierten Tönen. Per Zufall entdecke ich unter ihnen auch einen mit genau 2020 Hertz. Die untere Abbildung zeigt, dass der 2020 Hertz-Peak der Teekannendeckelglocke sehr viel schlanker ist der mit den Lippen erzeugte.
Nordwand-Qualität bedeuten, dass der Ton sehr rein ist. Auch damit kann ich dienen – allerdings mit einer anderen Art der Tonerzeugung: Der Deckel meiner Edelstahl-Teekanne sieht in etwa aus wie eine Glocke und klingt auch so. Beim Anschlag mit dem (Tee-)Löffel schwingt er mit einer ganzen Reihe von gut definierten Tönen. Per Zufall entdecke ich unter ihnen auch einen mit genau 2020 Hertz. Die untere Abbildung zeigt, dass der 2020 Hertz-Peak der Teekannendeckelglocke sehr viel schlanker ist der mit den Lippen erzeugte.
Ein Maß für die Schlankheit eines Ton-„Gebirges” ist der Quotient aus der Frequenz des Tons und der Breite des Peaks, bei der die Leistung auf den halben Wert des Maximums abgefallen ist. Dieser Quotient wird Güte Q (des schwingenden Systems) genannt. Ohne auf die Physik einzugehen: In unserer Darstellung der Intensität pro Frequenzintervall in der Einheit Dezibel (dB) ist die Breite bei halber Leistung die horizontale Ausdehnung des „Gebirges” 3 dB unterhalb des Gipfels. Danach hat das gepfiffene „Matterhorn” in Abbildung 1 eine Breite von etwa 18 Hz. Daraus folgt eine Güte von Q = 2020 Hz/18 Hz = 112. Beim Pfeifen schwingt die Mundhöhle als Helmholtz-Resonator, ein Q-Wert von etwa 100 erscheint in diesem Fall plausibel. Der Peak meiner Teekannendeckel-„Glocke” mit seinen „Eiger-Nordwand”-Flanken (Abbildung 2) hat eine Breite von rund 5,8 Hz und ergibt Q = 2020 Hz/5,8 Hz = 348, ein gegenüber dem Pfeifton dreifach größerer Wert. Der Q-Wert einer Kirchenglocke ist offenbar noch einmal um einen Faktor 3 bis 5 größer: Das mir vorliegende Spektrum1 eines Glockentons der Frequenz 697,5 Hz zeigt beispielsweise eine 3dB-Breite von 0,65 Hz, also Q = 1073. Eine andere Arbeit2 nennt Q-Werte von 1300, 1000 und 2000 bei den Frequenzen 624 Hz, 981 Hz bzw. 1310 Hz.
Als Kurzwellen-Amateur fühle ich mich natürlich verpflichtet, die Zahl 2020 auch im Kilohertz-Bereich zu realisieren: Hier die Beschreibung eines HF-Kreises aus Kondensator und Spule, der mit der Frequenz 2020 kHz schwingt.
1 J. Bauer: Ursachen des Missklangs von Glocken. Diplomarbeit, Fachhochschule Heidelberg, Fachbereich Informatik, Studiengang Elektrotechnik und md-pro GmbH Karlsruhe, Heidelberg 2003.
2 J. Woodhouse et al.: The Dynamics of a Ringing Church Bell, Advances in Acoustics and Vibration, Volume 2012, Article ID 681787, doi:10.1155/2012/681787
Neues Bauen in Gladbach-Rheydt
Noch ein Beitrag zum Jubiläum 100 Jahre Bauhaus: In meiner Heimatstadt Rheydt, damals Gladbach-Rheydt, steht etwas abseits der Straße das Schülerinnenwohnheim des Maria-Lenssen-Berufskollegs. Ein Highlight des Neuen Bauens, auch wenn es mit keinem der großen Namen Gropius, Meyer oder Mies van der Rohe verknüpft ist. Entworfen hat es der preußische Regierungsbaumeister Bruno Kleinpoppen, der Bau wurde Anfang der 30-er Jahre fertiggestellt. Inwiefern in dem Gebäude die Ideen des Bauhauses verwirklicht wurden, hat Birgit Gropp1 in hervorragender Weise beschrieben.
 Als Beitrag zum Jubiläum nehme ich mir vor, das Bauwerk noch einmal zu fotografieren – als bescheidene, aber persönliche Hommage an den Baumeister. Eine Gesamtansicht, wie ich sie von den Postkarten meiner Eltern her kenne, schwebt mir vor. Vor Ort stelle ich fest, dass daraus nichts wird: Bäume und Sträucher verdecken den Blick auf die volle Länge. Also nehme ich eine der alten Ansichtskarten hervor und zeichne das Gebäude ab.
Als Beitrag zum Jubiläum nehme ich mir vor, das Bauwerk noch einmal zu fotografieren – als bescheidene, aber persönliche Hommage an den Baumeister. Eine Gesamtansicht, wie ich sie von den Postkarten meiner Eltern her kenne, schwebt mir vor. Vor Ort stelle ich fest, dass daraus nichts wird: Bäume und Sträucher verdecken den Blick auf die volle Länge. Also nehme ich eine der alten Ansichtskarten hervor und zeichne das Gebäude ab.
1 Birgit Gropp: In Neues Bauen im Westen, https://www.baukunst-nrw.de
Durchblicke
… durch die Vorhangfassade am Bauhaus Dessau – fotografiert bei einem Besuch anlässlich des Jubiläums 100 Jahre Bauhaus. Wir werden durch das Bauhaus-Gebäude und die Meisterhäuser geführt. Dabei muss man dem Rudel folgen, so dass zum Fotografieren wenig Zeit bleibt. Die Ausbeute an guten Fotos ist deshalb dürftig. Hier einige Bilder zum Thema Glasfassade. Übrigens ist die Vorhangfassade (engl. curtain wall facade) keine Erfindung des Bauhauses. Die ersten Gebäude in Skelettbauweise mit vorgehängter Glasfassade wurden um 1900 gebaut.
Käfer auf Reise – 1969
Vor 50 Jahren (kleine Notiz zum Jubiläum): Eine Reise durch die USA mit dem VW-Käfer. Dauer etwa ein Monat, zurückgelegte Strecke 15000 km. Fotos (von links oben im Uhrzeigersinn): Abilene (Texas), Death Valley, Bluff (Utah), Yosemite Park, Rocky Mountains.
Route: New Haven – New Orleans – El Paso – Mesa Verde Natl Park – Monument Valley – Grand Canyon – Las Vegas – Death Valley – Los Angeles (Disneyland) – Monterey – San Francisco – Yosemite Natl Park – Salt Lake City – Grand Teton Natl Park – Yellowstone Natl Park – Devils Tower – Mt Rushmore – Badlands – Chicago – New Haven. Siehe auch hier.
Aus Neu mach Alt
 Der neugotische Harkness Tower der Yale-Universität in New Haven, CT (USA) ist schon eine Nachbildung. Er wurde nicht im Mittelalter, sondern in den Jahren 1917 bis1921 gebaut. Ich setze noch eins drauf: ein aktuelles Foto des Gebäudes wird auf alt getrimmt – „vintage look eines retro-Bauwerks“. Dazu benötigt man zunächst eine seitenverkehrte scharz-weiß-Kopie des Fotos. Die stellt mein Laserdrucker her. Ich lege ein etwas dickeres Papier bereit (etwa 200 g/m2), mindestens so groß wie die Fotokopie. Kopie und Papier werden mit Acryl-Binder bestrichen, mit der Klebeseite aufeinander gelegt, und mit viel Druck aufeineinander gepresst. Eine Gummiwalze hilft dabei. Ein heißes Bügeleisen sorgt nochmals für Druck und erhitzt den Binder, der dadurch austrocknet. Ich lasse das Papier-Sandwich noch etwas an der Luft trocknen und ziehe dann die Fotokopie vorsichtig ab: Mit etwas Glück befindet sich jetzt auf dem Papier eine (seitenrichtige) Kopie der (seitenverkehrten) Fotokopie. Kleine Bereiche, die nicht übertragen wurden, verstärken den vintage-Eindruck. Ich koloriere die Kopie der Fotokopie auf dem Papier mit Aquarellfarbe und bessere dabei die Übertragungsfehler aus. Das Ergebnis ist das Bild links.
Der neugotische Harkness Tower der Yale-Universität in New Haven, CT (USA) ist schon eine Nachbildung. Er wurde nicht im Mittelalter, sondern in den Jahren 1917 bis1921 gebaut. Ich setze noch eins drauf: ein aktuelles Foto des Gebäudes wird auf alt getrimmt – „vintage look eines retro-Bauwerks“. Dazu benötigt man zunächst eine seitenverkehrte scharz-weiß-Kopie des Fotos. Die stellt mein Laserdrucker her. Ich lege ein etwas dickeres Papier bereit (etwa 200 g/m2), mindestens so groß wie die Fotokopie. Kopie und Papier werden mit Acryl-Binder bestrichen, mit der Klebeseite aufeinander gelegt, und mit viel Druck aufeineinander gepresst. Eine Gummiwalze hilft dabei. Ein heißes Bügeleisen sorgt nochmals für Druck und erhitzt den Binder, der dadurch austrocknet. Ich lasse das Papier-Sandwich noch etwas an der Luft trocknen und ziehe dann die Fotokopie vorsichtig ab: Mit etwas Glück befindet sich jetzt auf dem Papier eine (seitenrichtige) Kopie der (seitenverkehrten) Fotokopie. Kleine Bereiche, die nicht übertragen wurden, verstärken den vintage-Eindruck. Ich koloriere die Kopie der Fotokopie auf dem Papier mit Aquarellfarbe und bessere dabei die Übertragungsfehler aus. Das Ergebnis ist das Bild links.
MAN WALKS ON MOON …
 schreibt die New York Times1 am 21. Juni 1969 – in mehr als 4 Zentimeter großen Lettern. Das war vor fünfzig Jahren, da ist eine kleine Notiz angebracht.
schreibt die New York Times1 am 21. Juni 1969 – in mehr als 4 Zentimeter großen Lettern. Das war vor fünfzig Jahren, da ist eine kleine Notiz angebracht.
Ich arbeitete damals als Physiker am Electron Accelerator Lab der Yale-Universität in New Haven, Connecticut (USA). Es ist Sonntag, der 20. Juli 1969. Mäßiges Wetter: Sonne, Wolken und, nicht unwichtig, Windstärke 4 bis 5. Denn ein Arbeitskollege lädt mich ein, mit ihm segeln zu gehen. Ich darf in seinem Boot die Fock bedienen. Der Yale Corinthian Yacht Club (YCYC) stellt seine Segeljollen an Feiertagen den Angestellten der Universität zur Verfügung. Davon machen einige sportlich gesinnte faculty-Leute Gebrauch und veranstalten Rennen auf dem Long Island Sound. An diesem Tag hat jedes Boot mindestens ein Transistorradio an Bord. Man ruft sich die neuesten Nachrichten zu, trotz Wettkampf. Die Meldung von der Landung (4.17 Uhr p.m. Eastern daylight time) dringt aber nicht bis zu uns durch – das Manöver, die letze Boje des Dreieckskurses zu umrunden erfordert unsere Aufmerksamkeit. Den historischen Zeitpunkt erfahren wir später von einem Boot, das querab segelt und uns gerade überholt. Am nächsten Morgen ist die New York Times so gut wie ausverkauft. Ich erstehe das letze von drei Exemplaren, die in der Lobby des Taft-Hotels ausliegen.
1 US-amerikanische Tageszeitung, erklärte Gegnerin von Donald Trump (Zitat des Herausgebers A.G. Sulzberger: „Wir werden [vor Trump] nicht auf die Knie fallen“, in DIE ZEIT vom 2. Mai 2019) – gut so.
Le Chemin de fer du Bocq
 Wir nehmen die Autobahn von Lüttich nach Charleroi. Bei Namur wechseln wir auf die E411 in Richtung Süden und erreichen nach etwa zehn Minuten den Ort Spontin. Spontin liegt am Bocq, einem Nebenfluss der Maas, der sich in einem waldreichen Tal durch die Ardennen windet. Durch das Tal führt auch eine Eisenbahnstrecke, der Chemin de fer du Bocq. Die Strecke verband früher die Orte Ciney und Yvoir (in Yvoir mündet der Bocq in die Maas). Sie ist schon seit Jahren für den Regelverkehr stillgelegt, wird aber als Museumslinie intensiv genutzt. Der Verein, der die historischen Fahrten veranstaltet, ist der Patrimoine Ferroviaire et Tourisme (PFT) – oder, in niederländisch, Toerisme en Spoorpatrimonium (TSP).
Wir nehmen die Autobahn von Lüttich nach Charleroi. Bei Namur wechseln wir auf die E411 in Richtung Süden und erreichen nach etwa zehn Minuten den Ort Spontin. Spontin liegt am Bocq, einem Nebenfluss der Maas, der sich in einem waldreichen Tal durch die Ardennen windet. Durch das Tal führt auch eine Eisenbahnstrecke, der Chemin de fer du Bocq. Die Strecke verband früher die Orte Ciney und Yvoir (in Yvoir mündet der Bocq in die Maas). Sie ist schon seit Jahren für den Regelverkehr stillgelegt, wird aber als Museumslinie intensiv genutzt. Der Verein, der die historischen Fahrten veranstaltet, ist der Patrimoine Ferroviaire et Tourisme (PFT) – oder, in niederländisch, Toerisme en Spoorpatrimonium (TSP).
Wir haben uns beim PFT (TSP) zu einer Eisenbahn-Fotosafari angemeldet. Sie startet am Bahnhof Spontin und bringt uns zu den schon etablierten Kamera-Standorten entlang der Strecke. Dort herrscht Disziplin. Oberstes Gebot ist: Niemand läuft dem Anderen vor die Kamera. Es gibt, wie beim Freistoß auf dem Fußballfeld, eine Linie, die in Richtung auf das Objekt (Lok, Zug, Triebwagen) nicht überschritten wird. Wer es tut, outet sich als Neuling, der die Regeln nicht kennt. Die besten Foto-Standorte sind Viadukte mit Tunnelportalen im Hintergrund (Abbildung).
Rietveld Schröder Haus
Das Bauhaus wird in diesem Jahr 100. Vielleicht sollte man nicht vergessen, dass zeitgleich zum Bauhaus auch abseits von Weimar und Dessau moderne Architektur entwickelt wurde. Ein Beispiel: das Rietveld Schröder-Haus in Utrecht (Niederlande), gebaut 1924 nach den Prinzipien von De Stijl. Gerrit Rietveld (1888 – 1964) war der Architekt, Frau T. Schröder (1889 – 1985) die Bewohnerin. Das Haus wurde im Jahr 2000 von der UNESCO in die Liste der Weltkulturstätten aufgenommen. Gestern war es grau und regnerisch – für ein Foto gar nicht so schlecht, an solchen Tagen gibt es schöne gesättigte Farben. Weitere Bilder unten.
2019 – ein (Oster-)paradoxes Jahr
 Dieses Jahr ist es der Kalender, der aus dem Rahmen fällt: 2019 feiern wir Ostern nicht an dem Tag, an dem das Fest eigentlich stattfinden sollte – 2019 ist ein Jahr mit einem Oster-Paradox.
Dieses Jahr ist es der Kalender, der aus dem Rahmen fällt: 2019 feiern wir Ostern nicht an dem Tag, an dem das Fest eigentlich stattfinden sollte – 2019 ist ein Jahr mit einem Oster-Paradox.
Ostern, so lernt man, fällt auf den ersten Sonntag nach dem ersten Vollmond nach Frühlingsanfang. Der Frühlingsanfang ist der Zeitpunkt, an dem die Sonne auf ihrer Bahn den Himmelsäquator aufsteigend durchstößt. Der so definierte astronomische Frühlingsanfang kann auf den 19., 20. oder 21. März fallen. Aber Ostern ist ein christliches Fest, deshalb hatte die Kirche ein Mitspracherecht bei der Terminvergabe: sie legte den Frühlingsanfang unverrückbar auf den 21. März. Das geschah schon im Jahr 325 auf dem Konzil von Nikäa (heute Iznik, Türkei). Im Zuge der Kalenderreform 1582 wurde zudem ein Rechenverfahren erarbeitet, das die Vollmondphasen näherungsweise vorhersagt. Es wurde zur Festlegung des Osterdatums verbindlich vorgeschrieben und ist als Datumsregel nach dem Kirchenzyklus bekannt. Später entwickelte C. F. Gauss aus dieser Regel einen Algorithmus, nach dem sich das Osterdatum berechnen lässt.
Diese Regel führt 2019 zu einer ungewöhnlichen Situation: Der astronomische Frühling beginnt am 20. März 2019, 22:58 Uhr MEZ, also durchaus normgerecht. Das Problem ist, dass unser Trabant schon kurz danach (also kurz nach dem 20. März, 22:58 Uhr MEZ) die Phase „Vollmond” erreicht, nämlich am 21. März, 2:43 Uhr MEZ. Ostern müsste daher, astronomisch gesehen, auf den darauf folgenden Sonntag, den 24. März fallen. Tatsächlich ist aber nach dem Kirchenzyklus (und nach dem Rechenverfahren von Gauss) Ostern am 21. April, also vier Wochen später. Diese Datumsverschiebung ist das Oster-Paradox.
Es ist interessant, die astronomischen Daten am (Personal-)Computer nachzurechnen. Dazu gibt es in der Literatur Programme, zum Beispiel die von O. Montenbruck und Th. Pfleger1. Mehr zum Osterparadoxon und zu den Computer-Rechnungen hier.
1 Oliver Montenbruck und Thomas Pfleger: Astronomie mit dem Personal Computer, 3. Auflage, J. Springer, Berlin-Heidelberg-NewYork, 1999. Ein hervorragendes Buch, nicht nur für Experten.