Ein LC-Kreis ist ein elektromagnetischer Schwingkreis, bestehend aus der Parallelschaltung einer Spule und eines Kondensators. Die Abkürzung LC bedeutet Spule-Kondensator: L ist das Formelzeichen für eine Induktivität (Spule), C das Zeichen für eine Kapazität (Kondensator). Trägt man den Wechselstromwiderstand eines LC-Kreises als Funktion der Frequenz auf, erhält man die sogenannte Resonanzkurve.
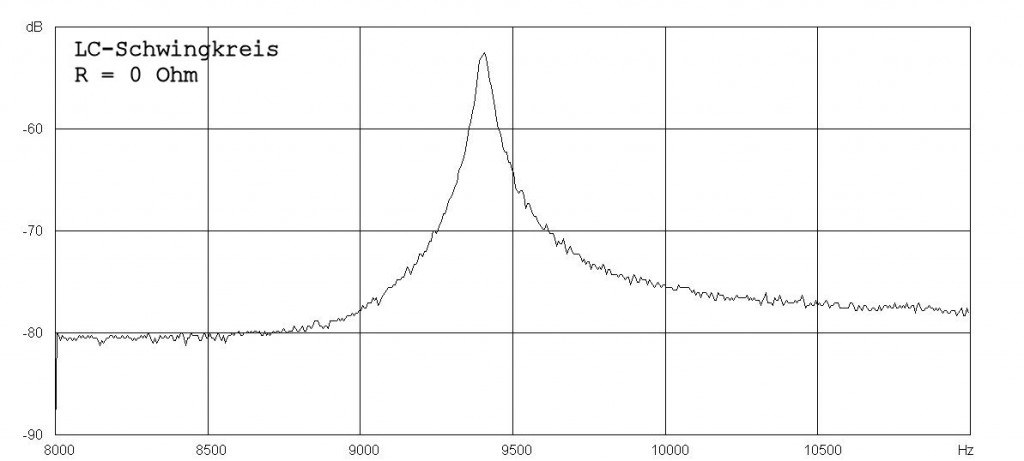
Abbildung 1 zeigt das Beispiel einer Resonanzkurve, die mithilfe der Soundkarte eines Computers aufgenommen wurde. Der Messaufbau ist aus Abb. 2 ersichtlich. Schwingkreis und Pufferstufe sind auf einer Experimentierplatine (Hirschmann) aufgebaut. Für die Physik von Interesse ist beispielsweise die Abhängigkeit der Breite dieser Kurve (Bandbreite) vom Verlustwiderstand des LC-Kreises. Sicher keine aufregende Untersuchung, aber als Experimentierübung bestens geeignet. Hier eine kurze Zusammenfassung der Theorie und die Auswertung einer Messreihe dazu – als Beispiel für eine Facharbeit in der Jahrgangsstufe Q1 des Gymnasiums.