Auf dem Übungsprogramm steht zur Zeit die Lasurtechnik. Hier erste Ergebnisse, noch verbesserungsbedürftig.
Monat: November 2013
Ulams Primzahlspirale
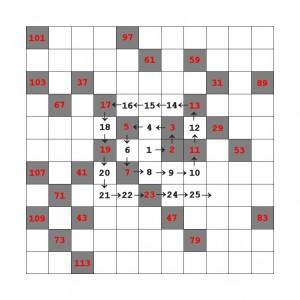
Ulams (viereckige) Primzahlspirale. Die natürlichen Zahlen werden, in der Mitte mit 1 beginnend, der Reihe nach spiralförmig im Gegenuhrzeigersinn eingetragen. Hier sind es die Zahlen bis einschließlich 121 in der rechten unteren Ecke.
Wir nehmen ein Blatt kariertes Papier zur Hand und tragen die natürlichen Zahlen der Reihe nach in die Karos ein. Den Anfang macht die 1 in der Mitte des Blattes. Rechts davon wird die 2 platziert, im Kästchen darüber die 3 und links davon die beiden Zahlen 4 und 5. Die 6 und 7 belegen die Karos unterhalb der 5, und die 8 wird rechts von der 7 eingetragen, usw. Das heißt, wir bewegen uns im Gegenuhrzeigersinn auf einer (viereckigen) Spirale nach außen. Geraten wir an eine Primzahl, wird das zugehörige Kästchen farbig markiert.
Das Ergebnis sollte dann aussehen wie in der Abbildung.
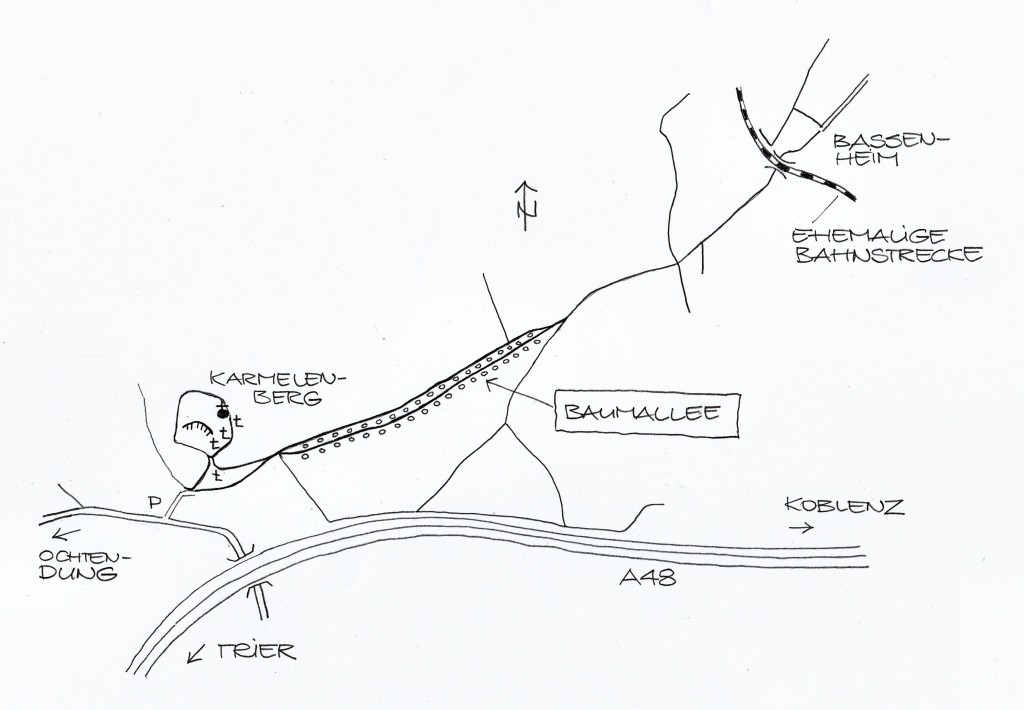
Naturdenkmal Baumallee Bassenheim
Bassenheim ist ein linksrheinischer Ort in der Nähe von Koblenz. Von dort geht in Richtung Westen ein Fußweg zu einem alten Vulkankegel, auf der Karte als „Karmelenberg“ bezeichnet. Der Weg unterquert den Viadukt einer stillgelegten Eisenbahnstrecke, durchläuft ein kurzes Stück Wald und mündet dann in eine Allee von zum Teil uralten Bäumen – ein faszinierender Anblick. Die Fotos sind keine Meisterwerke – beiläufig aufgenommen beim Wandern auf dem Rheinburgenweg. Der etwas seltsam anmutende Name „Karmelenberg“ leitet sich her, wie man liest, vom Berg Karmel im Norden Israels. Im Alten Testament wird berichtet, dass Elia dort das Gottesurteil gegen die Propheten des Baal herbeiführte (1. Kön 18). Offenbar gibt es noch mehr Stätten, die nach dem Berg in Israel benannt sind. Zum Beispiel der Ort Carmel-by-the-Sea (bei Monterey, Californien, USA) und die dortige Missionsstation Carmel Mission.
Perfektes Quadrat
Ein Quadrat ist ein rechtwinkliges Viereck mit vier gleich langen Seiten. Ein perfektes Quadrat ist ein Quadrat, das sich vollständig in kleinere Quadrate aufteilen lässt, wobei keine zwei dieser Teilquadrate einander gleich sein dürfen – oder, etwas mathematischer formuliert: Ein Quadrat, das sich in lauter paarweise verschieden große Quadrate zerlegen lässt, heißt perfekt.
Die Abbildung zeigt Exemplare des perfekten Quadrats der Ordnung 21. Es enthält 21 paarweise verschiedene Teilquadrate – mit unterschiedlichen Farben ausgemalt. Mehr…
Wandern auf dem Rheinburgenweg
Eine kleine Sammlung von Fotos vom linksrheinischen Rheinburgenweg zwischen Bingen und Mehlem. Auch hier war ich in einzelnen Tagesetappen unterwegs. Ein Highlight: der Blick auf die Loreley vom Aussichtspunkt Maria Ruh.
