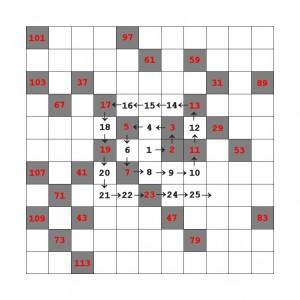
Ulams (viereckige) Primzahlspirale. Die natürlichen Zahlen werden, in der Mitte mit 1 beginnend, der Reihe nach spiralförmig im Gegenuhrzeigersinn eingetragen. Hier sind es die Zahlen bis einschließlich 121 in der rechten unteren Ecke.
Wir nehmen ein Blatt kariertes Papier zur Hand und tragen die natürlichen Zahlen der Reihe nach in die Karos ein. Den Anfang macht die 1 in der Mitte des Blattes. Rechts davon wird die 2 platziert, im Kästchen darüber die 3 und links davon die beiden Zahlen 4 und 5. Die 6 und 7 belegen die Karos unterhalb der 5, und die 8 wird rechts von der 7 eingetragen, usw. Das heißt, wir bewegen uns im Gegenuhrzeigersinn auf einer (viereckigen) Spirale nach außen. Geraten wir an eine Primzahl, wird das zugehörige Kästchen farbig markiert.
Das Ergebnis sollte dann aussehen wie in der Abbildung. Dort ist die Windung der Spirale für die Zahlen < 26 durch Pfeile angedeutet. Grau unterlegte Karos: Primzahlen (der Zahlenwert ist in Rot eingetragen). Sie häufen sich auf diagonal verlaufenden Geraden. Die Sequenzen 5, 19, 41, 71, 109 und 7, 19, 23, 47, 79 bilden sogar zusammenhängende Geradenabschnitte in Diagonalrichtung.
Von Interesse ist die Frage, ob sich aus den Primzahlketten der Ulamschen Spirale Formeln für Primzahlfolgen herauslesen lassen. Das ist in der Tat der Fall. Die Reihe der Primzahlfelder beispielsweise, die bei 5 beginnt und sich in Richtung links unten fortsetzt (siehe Abbildung), enthält die Primzahlen 5, 19, 41, 71, 109. Sie lässt sich durch den Term 4n2 + 10n + 5 erzeugen, wenn man für n die Zahlen 0 bis 4 einsetzt. Der nächste, für n = 5 erzeugte Wert wäre 155 und damit keine Primzahl. Auch das Eulersche Primzahl-Polynom n2 + n + 41 liefert (zumindest bei größeren Platznummern n) zusammenhängende Diagonalenabschnitte mit Primzahlen. Mehr
