Monat: Januar 2020

Lichtgeschwindigkeit

 in Physik als Hobby

An das Workshop erinnere ich mich noch (lang ist’s her): Eine Gruppe von Physiklehrern versucht, mit Lötkolben und Seitenschneider ausgestattet, unter der Anleitung ihres Kollegen U. Ihlefeldt die Elektronik für eine Apparatur zusammenzubauen, mit der man die Lichtgeschwindigkeit im Labor messen kann. Ich bin dabei – und am Ende der Veranstaltung glücklich, zwei funktionierende Schaltungen mit nach Hause nehmen zu können.
Die Elektronik bestand aus einem Lichtsender und einem Lichtempfänger, mit denen man unter Zuhilfenahme eines schnellen Oszilloskops die Zeit messen konnte, die das Licht zum Zurücklegen einer gegebenen Strecke benötigt. Zur Messanordnung gehörten außerdem ein (halbdurchlässiger) Spiegel, ein Reflektor und eine Linse. Trotz des geringen Aufwandes, den die Apparatur erforderte, lieferte sie recht gute Werte. Bei genauerer Messung stellte ich allerdings fest, dass sie systematisch einen Tick größer waren als die bekannten 300000 km/s.
Vor kurzem fiel mir die Apparatur wieder in die Hände – Grund genug, sie nochmals aufzubauen und auch nochmals zu messen. Das Foto zeigt den aktuellen Messaufbau mit Lichtsender, halbdurchlässigem Spiegel, Empfänger und einem Epidiaskop-Objektiv als Linse. Das Licht wird nach Durchlaufen einer gewissen Strecke zurückgeworfen (der Reflektor ist nicht zu sehen) und durch den halbdurchlässigen Spiegel in den Empfänger umgelenkt. Das Oszilloskop misst die Phasenverschiebung zwischen ausgesandtem und vom Empfänger registriertem Lichtimpuls. Durch den Einsatz des Epidiaskop-Objektivs konnte ich das Licht besser bündeln als in der ursprünglichen Anordnung. Infolgedessen wurde mehr Licht in den Empfänger zurückgelenkt, so dass sich die Zeitspanne zwischen Aussendung und Rückkehr des Lichtimpulses sehr genau messen ließ.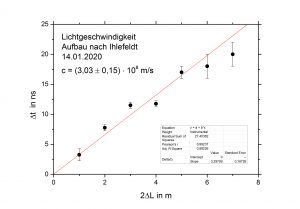

Offenbar führt der Intensitätsgewinn auch zu Messwerten, die dem Literaturwert der Lichtgeschwindigkeit näherkommen – also nicht mehr systematisch nach oben abweichen. Das Diagramm zeigt das Ergebnis einer Messung mit der verbesserten Apparatur. Aufgetragen ist die „Reisezeit” Δt des Lichts in Abhängigkeit von der Laufstrecke 2ΔL, wobei die eingezeichnete Ausgleichsgerade einer Lichtgeschwindigkeit von (3,03 ± 0,15) ×108 m/s entspricht. Die Fehlergrenzen ± 0,15 ×108 m/s ergeben sich aus der Streuung der Messpunkte um die Gerade. Eine größere Genauigkeit als die angegebenen ± 5% lässt sich mit der Anordnung wohl kaum erreichen. Etwas mehr zu diesem Experiment hier.

2020 – das Jahr mit dem Pfiff

 in Physik als Hobby, Verschiedenes

Eine etwas skurrile Performance: Wir beginnen das neue Jahr mit einem mit den Lippen erzeugten Pfeifton der Tonhöhe (Frequenz) von genau 2020 Hertz (typischer Einfall eines Physikers). In meinem PC ist, wie üblich, ein Mikrofon eingebaut, dessen Signal in einer Soundkarte digitalisiert wird. Das digitalisierte Signal wird nach der Tonhöhe sortiert (Fourier-analysiert) und das Spektrum der Tonhöhen auf dem Bildschirm dargestellt. In dieser Anordnung lässt sich die Frequenz des Pfeiftons messen. Ich beobachte also, während ich drauflos pfeife, das Tonhöhengebirge auf dem Computer-Bildschirm. Änderungen in der Lage von Zunge und Unterkiefer ergeben verschiedene Tonhöhen. Nach etwas Übung zeigt sich tatsächlich ein Matterhorn-ähnlicher Peak bei 2020 Hertz: Treffer (Abbildung oben). – Ein kleiner Mangel: Das Matterhorn dürfte etwas schroffer sein. Physiker bevorzugen Peaks mit steileren Flanken. Peaks mit Flanken in Eiger-Nordwand-Qualität bedeuten, dass der Ton sehr rein ist. Auch damit kann ich dienen – allerdings mit einer anderen Art der Tonerzeugung: Der Deckel meiner Edelstahl-Teekanne sieht in etwa aus wie eine Glocke und klingt auch so. Beim Anschlag mit dem (Tee-)Löffel schwingt er mit einer ganzen Reihe von gut definierten Tönen. Per Zufall entdecke ich unter ihnen auch einen mit genau 2020 Hertz. Die untere Abbildung zeigt, dass der 2020 Hertz-Peak der Teekannendeckelglocke sehr viel schlanker ist der mit den Lippen erzeugte.

Ein Maß für die Schlankheit eines Ton-„Gebirges” ist der Quotient aus der Frequenz des Tons und der Breite des Peaks, bei der die Leistung auf den halben Wert des Maximums abgefallen ist. Dieser Quotient wird Güte Q (des schwingenden Systems) genannt. Ohne auf die Physik einzugehen: In unserer Darstellung der Intensität pro Frequenzintervall in der Einheit Dezibel (dB) ist die Breite bei halber Leistung die horizontale Ausdehnung des „Gebirges” 3 dB unterhalb des Gipfels. Danach hat das gepfiffene „Matterhorn” in Abbildung 1 eine Breite von etwa 18 Hz. Daraus folgt eine Güte von Q = 2020 Hz/18 Hz = 112. Beim Pfeifen schwingt die Mundhöhle als Helmholtz-Resonator, ein Q-Wert von etwa 100 erscheint in diesem Fall plausibel. Der Peak meiner Teekannendeckel-„Glocke” mit seinen „Eiger-Nordwand”-Flanken (Abbildung 2) hat eine Breite von rund 5,8 Hz und ergibt Q = 2020 Hz/5,8 Hz = 348, ein gegenüber dem Pfeifton dreifach größerer Wert. Der Q-Wert einer Kirchenglocke ist offenbar noch einmal um einen Faktor 3 bis 5 größer: Das mir vorliegende Spektrum1 eines Glockentons der Frequenz 697,5 Hz zeigt beispielsweise eine 3dB-Breite von 0,65 Hz, also Q = 1073. Eine andere Arbeit2 nennt Q-Werte von 1300, 1000 und 2000 bei den Frequenzen 624 Hz, 981 Hz  bzw. 1310 Hz.

Als Kurzwellen-Amateur fühle ich mich natürlich verpflichtet, die Zahl 2020 auch im Kilohertz-Bereich zu realisieren: Hier die Beschreibung eines HF-Kreises aus Kondensator und Spule, der mit der Frequenz 2020 kHz schwingt.

1   J. Bauer: Ursachen des Missklangs von Glocken. Diplomarbeit, Fachhochschule Heidelberg, Fachbereich Informatik, Studiengang Elektrotechnik und md-pro GmbH Karlsruhe, Heidelberg 2003.

2  J. Woodhouse et al.: The Dynamics of a Ringing Church Bell, Advances in Acoustics and Vibration, Volume 2012, Article ID 681787, doi:10.1155/2012/681787