Zur Abwechslung Physik: Es geht wieder einmal um den Q-Wert eines Schwingkreises aus Spule (Induktivität L) und Kondensator (Kapazität C). In diesem Fall ist es ein Parallelkreis. Im Ersatzschaltbild fügen wir noch einen Widerstand parallel zu Spule und Kondensator hinzu. Sein Wert R stellt die Ohmschen Verluste des Kreises dar. Die Aufgabe lautet, den Gütefaktor Q dieses RLC-Kreises durch eine Reflexionsmessung zu bestimmen. Ich benutze dazu meinen kürzlich erstandenen Antennen-Analysator1 FA-VA 5, ein Gerät, das eine elektromagnetische Welle über ein Kabel dem zu untersuchenden Bauteil zuführt und ermittelt, welcher Anteil der Welle vom Bauteil zurückgeworfen wird. Die vom Analysator gemessene Größe ist eine komplexe Zahl, genannt Reflexionsfaktor S11, und wird nach Betrag und Phase ermittelt. S11 hängt ab von der Frequenz f, mit der der RLC-Kreis angeregt wird, und wird in der Regel als Ortskurve – mit f als Parameter – in der komplexen Zahlenebene (Smith-Diagramm) dargestellt.
Die Idee zu dieser Messung entstand beim Stöbern in Internet: Ich stieß auf die Versuchsanleitung zu einem Experiment des Physik-Praktikums an der TU Darmstadt2. Dort sollte mit Hilfe des Reflexionsverfahrens der Q-Wert eines HF-Resonators bestimmt werden. Das Institut für Kernphysik der TU Darmstadt benutzt solche Resonatoren an seinem Elektronenbeschleuniger S-DALINAC. In jungen Jahren habe ich selber längere Zeit an diesem Institut gearbeitet (am Vorgänger-Beschleuniger DALINAC). Es freut mich also, in dieser Sache noch einmal an meine ehemalige Arbeitsstätte erinnert zu werden.
Der RLC-Parallelkreis ist das übliche Ersatzschaltbild eines HF-Resonators im Fall von Reflexionsmessungen. Was als Ersatzschaltbild taugt, sollte sich auch in der Realität bewähren. Die Frage (siehe oben) ist also: Kann man den Gütefaktor Q eines RLC-Kreises durch eine Reflexionsmessung bestimmen?
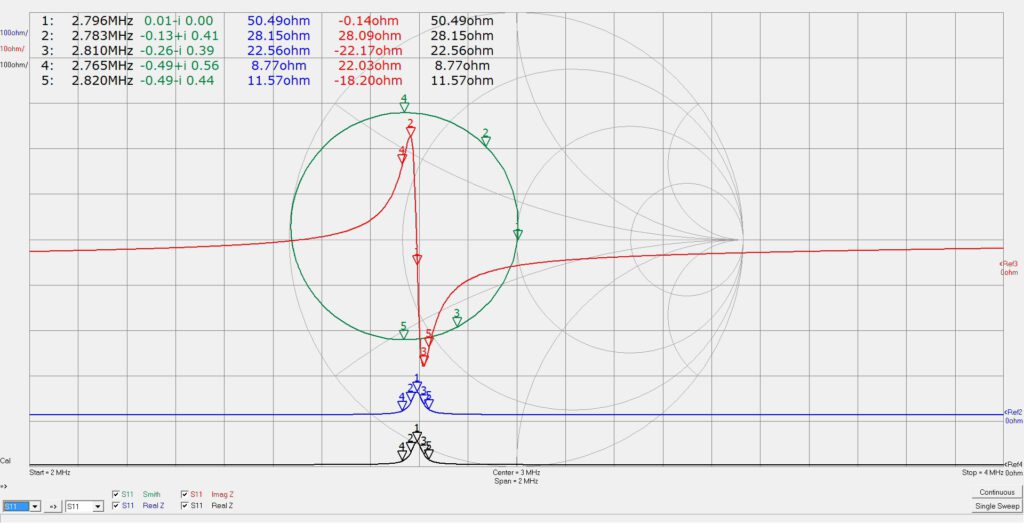
Mein RLC-Schwingkreis besteht aus einer Luftspule mit der Induktivität L = 10 μH und einem Keramik-Kondensator der Kapazität C = 330 pF. Nach der Thomsonschen Formel sollte seine Resonanzfrequenz f0 = 2,77 MHz betragen – gemessen wurden 2,796 MHz. Ohne auf Theorie und Details der Messung3 einzugehen, hier das Ergebnis meines (Hobby-)Experiments: Die Abbildung zeigt, als Funktion der Frequenz, den Reflexionsfaktor S11 und die Impedanz Z des RLC-Kreises – und zwar in unterschiedlichen Koordinatensystemen. Die Ortskurve des S11-Faktors (grüne Kurve) ist im Smith-Diagramm dargestellt, während die Impedanz, aufgeteilt in
Realteil (blaue oder schwarze Kurve) und Imaginärteil (rote Kurve) in dem zusätzlich eingezeichneten kartesischen Koordinatensystem abzulesen ist. Gemessen wurde im Frequenzintervall zwischen 2 und 4 MHz. Von den eingezeichneten Frequenzmarken interessieren hier die Resonanzfrequenz f0 = 2,796 MHz (Marke 1) und die beiden –3dB-Frequenzen f2 = 2,783 MHz und f3 = 2,810 MHz (Marken 2 und 3). Daraus ergibt sich eine Bandbreite von Δf = f3 – f2 = 0,027 MHz, der Gütefaktor Q = f0/Δf ist damit Q = 104. Zur Kontrolle bestimmte ich mit einem Rauschgenerator die Filterkurve (Resonanzkurve) des RLC-Kreises. Deren Resonanzfrequenz war f0 = 2,792 MHz, ihre Bandbreite Δf = 0,0265 MHz. Daraus folgt als Gütefaktor Q = 107.
Das professionelle Experiment an einem HF-Resonator (an Stelle eines RLC-Schwingkreises) wird in einem Vortrag am CERN beschrieben4.
1 Der Vektor-Antennen-Analysator FA-VA 5 wird in Amateurfunk-Kreisen als Bausatz gehandelt. Er wurde von Michael Knitter (DG5MK) entworfen, die Software zur Anbindung des Geräts an einen PC und zur Darstellung der Ergebnisse auf dem Bildschirm stammt von Thomas Baier (DG8SAQ).
2 Versuch 1.2 – Hochfrequenzresonatoren, Physikalisches Praktikum für Fortgeschrittene, Institut für Kernphysik, TU Darmstadt. www.ikp.tu-darmstadt.de› ikp › lehre_ikp › vers12
3 Eine ausführliche Beschreibung der Messungen hier.
4 Antonio G., Markus J., Hélène G. und Alex S.: RF Cavity experiments, CERN, Presentation_RF_AG_MJ_HG_AS.pdf, indico.cern.ch