Im Juni 1980 erschien im „Spektrum der Wissenschaft” (der deutschen Ausgabe des Scientific American) ein Artikel von Martin Gardner1 mit dem Titel „Weiße und braune Melodien, Schachtelkurven und 1/f-Fluktuationen”. Gardner stellte darin die Arbeit eines Physikers vor – sein Name ist Richard F. Voss2, der eine interessante Beziehung zwischen Musik („weiße und braune Melodien”) und zufälligen Schwankungen einer besonderen Art („1/f-Fluktuationen”) entdeckte. Zufällige Schwankungen heißen in der Physik üblicherweise „Rauschen”. Es geht also um den Zusammenhang zwischen Musik und Rauschen.
Musik erfreut (in der Regel), Rauschen nervt (meistens). Ob ein Lautsprecher Musik oder Rauschen liefert, hängt vom zeitlichen Verlauf der (niederfrequenten, NF-) Wechselspannung ab, die an der Lautsprecherspule anliegt. Folgt die Spannung einer Melodie, handelt es sich um Musik, schwankt sie zufällig, um Rauschen. Dieses Rauschen, das durch die zufälligen Schwankungen der Spannung V(t) des NF-Signals zustande kommt, ist hier nicht von Interesse. Hier geht es vielmehr um die zeitlichen Änderungen, die dem Auf und Ab der Lautstärke und der Tonhöhe in einem Musikstück entsprechen. Auch das sind Schwankungen – sie sind aber offenbar weniger oder nur zum Teil zufällig, stellen also eine andere Art Rauschen dar als die Schwankungen von V(t). Man kann sie aber aus dem Zeitverhalten dieses Signals, also aus V(t), ableiten: Die momentane Lautstärke des Signals ist proportional zur Leistung, und diese wiederum proportional zu V2(t). Die momentane Tonhöhe ist proportional zur momentanen Frequenz, und diese wiederum proportional zur Rate Z(t), mit der die Spannung das Vorzeichen wechselt, also proportional zur Zahl der Nulldurchgänge pro Sekunde (Nulldurchgangsrate, engl. zero crossing rate). Lautstärke- und Tonhöhenfluktuationen spiegeln sich also in den Größen V2(t), der Audioleistung, beziehungsweise der Nulldurchgangsrate Z(t) wider.
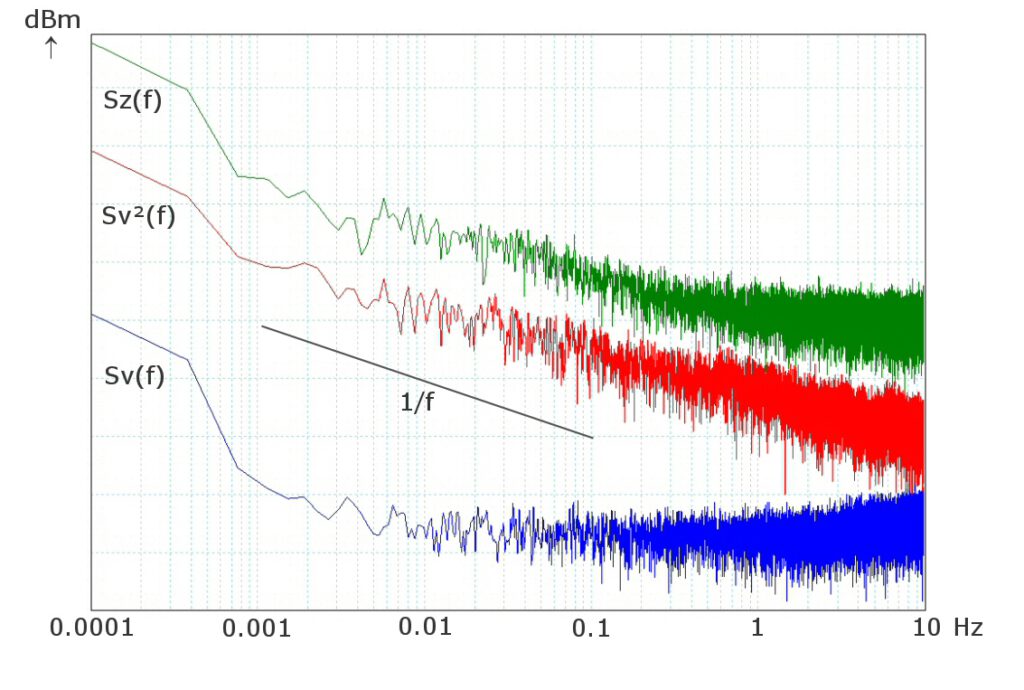
Beide Größen, V2(t) und Z(t), werden nach Fourier zerlegt. Ihre Fouriertransformierten SV²(f) beziehungsweise SZ(f) geben an, mit welcher Intensität ein kleines Frequenzintervall, dessen Mitte die Frequenz f ist, zur Schwankung der entsprechenden Größe im Musikstück beiträgt. Eine Intensität pro Frequenzintervall heißt üblicherweise spektrale Dichte, SV²(f) und SZ(f) sind daher die spektralen Dichten der Lautstärke (Audioleistung) beziehungsweise momentanen Tonhöhe (Nulldurchgangsrate). Von Interesse ist deren Abhängigkeit von der Frequenz. Voss’ Ergebnis lautet: Die spektrale Dichte der Lautstärke- und Tonhöhenfluktuationen von Musik nimmt umgekehrt proportional zur Frequenz ab. Sie verhält sich, mathematisch ausgedrückt, wie die Funktion 1/f – daher der Name „1/f -Fluktuationen“. Stellt man sie in doppelt-logarithmischem Koordinatenpapier dar, ergibt sich eine Gerade mit der Steigung –1.
In die Sprache der Musik übersetzt, heißt das: Langsame Schwankungen von Lautstärke und Tonhöhe, sie entsprechen kleinen Frequenzen in SV²(f) und SZ(f), überwiegen gegenüber schnellen Änderungen, das heißt hohen Frequenzen in SV²(f) und SZ(f). Kleine Änderungen von Lautstärke und Tonhöhe kommen weitaus öfter vor als große Sprünge. Voss hat 1/f-Fluktuationen von Lautstärke und Tonhöhe in verschiedenen Arten von Musik nachgewiesen: Klassik, Jazz, Rock und Pop. Im Übrigen untersuchte er auch Nachrichtensendungen und Aufzeichnungen von Reden, also Sprache, im Hinblick auf derartige Fluktuationen. Sie sind, wie er feststellte, jedoch anderer Art.
Ich habe einen Teil der Voss’schen Experimente versucht nachzuahmen – schon vor einigen Jahren. Aktuelle Experimente haben meine früheren Ergebnisse bestätigt. Die Abbildung zeigt die von mir kürzlich gemessenen spektralen Dichten der Lautstärke- und Tonhöhenfluktuationen in den Brandenburgischen Konzerten und Orchestersuiten von J. S. Bach (Diese Musikstücke hatte auch Voss analysiert). Die rote Kurve stellt die Dichte SV2(f) der Lautstärkeschwankungen, die grüne Kurve die Dichte SZ(f) der Tonhöhenschwankungen dar. Beide Kurven zeigen, wie bei Voss, einen 1/f -Verlauf. Um den Unterschied zwischen den Fluktuationen von Audioleistung V2(t) und Nulldurchgangsrate Z(t) auf der einen und Signalspannung V(t) auf der anderen Seite deutlich zu machen, wurde in der Abbildung auch die Dichte von V(t) dargestellt (blaue Kurve, mit SV(f) bezeichnet). Sie ist im dargestellten Frequenzbereich und auch oberhalb von 10 Hz von der Frequenz unabhängig („weißes Rauschen”). – Mehr Rauschen hier.
1 Martin Gardner: Mathematische Spielereien – Weiße und brauen Melodien, Schachtelkurven und 1/f-Fluktuationen, Spektrum der Wissenschaft („Scientific American”), Juni 1980, S. 14
2 Richard F. Voss und John Clarke: 1/f noise in music: Music from 1/f noise, J. Acoust. Soc. Am. 63(1), Jan. 1978, p. 258
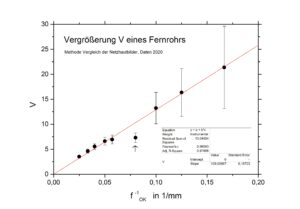
 Wenn ich von meinem Fernrohr erzählte, fragte man geradezu zwangsläufig nach dessen Vergrößerung. Nun, die Vergrößerung eines astronomischen Fernrohrs interessiert zwar, ist in der Regel aber zweitrangig (In der Hauptsache geht es darum, das optische Signal-zu-Rausch-Verhältnis anzuheben). Jedenfalls habe ich im Physikunterricht seinerzeit meine Schüler und Schülerinnen die Vergrößerung eines kleinen Fernrohr-Modells bestimmen lassen. Es bestand aus einem Objektiv, herausgeschraubt aus einem 8×30-Fernglas, mit einem Tubus, an dessen Ende ich eine 31-mm-Steckfassung zur Aufnahme verschiedener Okulare¹ angebracht hatte. Die Okulare waren Exemplare aus dem Okularsatz meines (Refraktor-)Fernrohrs.
Wenn ich von meinem Fernrohr erzählte, fragte man geradezu zwangsläufig nach dessen Vergrößerung. Nun, die Vergrößerung eines astronomischen Fernrohrs interessiert zwar, ist in der Regel aber zweitrangig (In der Hauptsache geht es darum, das optische Signal-zu-Rausch-Verhältnis anzuheben). Jedenfalls habe ich im Physikunterricht seinerzeit meine Schüler und Schülerinnen die Vergrößerung eines kleinen Fernrohr-Modells bestimmen lassen. Es bestand aus einem Objektiv, herausgeschraubt aus einem 8×30-Fernglas, mit einem Tubus, an dessen Ende ich eine 31-mm-Steckfassung zur Aufnahme verschiedener Okulare¹ angebracht hatte. Die Okulare waren Exemplare aus dem Okularsatz meines (Refraktor-)Fernrohrs.