Monat: September 2013

UKW-Rundfunksender arbeiten mit einer Frequenz von etwa 100 MHz. Es gibt aber auch „Radiowellen“ (elektromagnetische Schwingungen) mit sehr viel kleinerer Frequenz. Zum Beispiel 8 Hz – das heißt 8 Schwingungen in einer Sekunde. Sie werden Schumann-Resonanzen genannt, nach W. O. Schumann¹, der sie 1952 aufgrund theoretischer Rechnungen voraussagte.

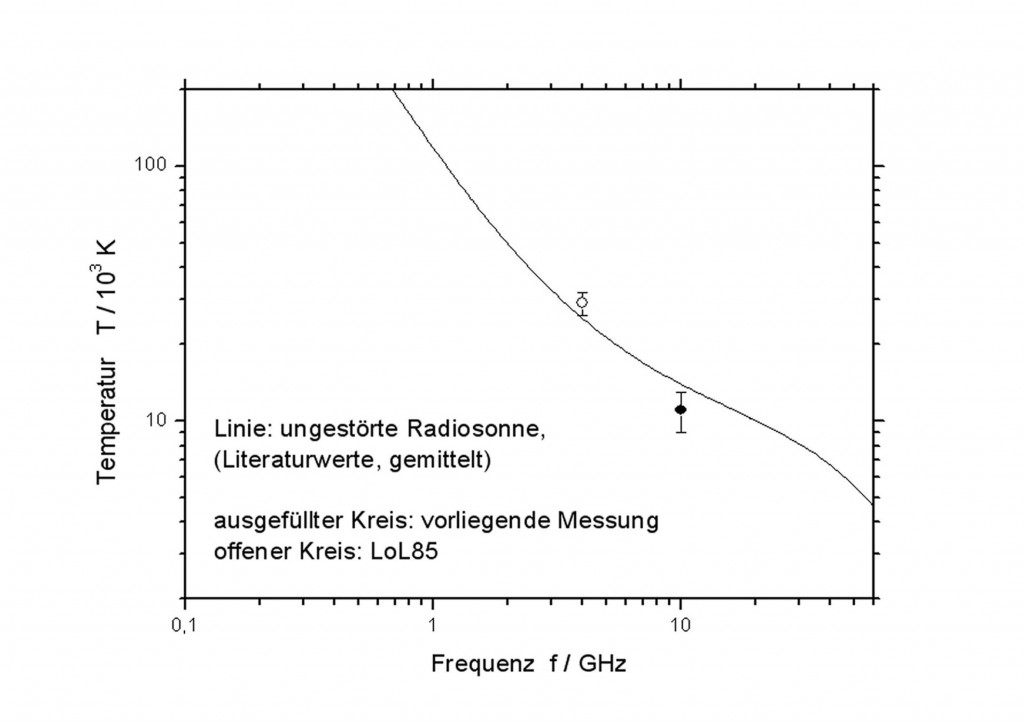
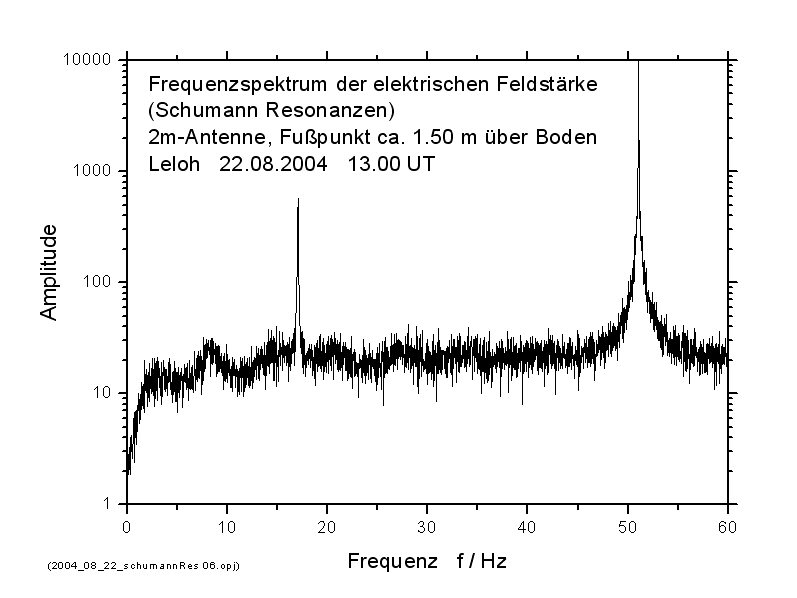
Die Schumann-Resonanzen sind stehende Wellen, die sich zwischen der Erdoberfläche und der Ionosphäre ausbilden. Sie werden durch die Blitze der Gewitter angeregt, die ständig auf der Erde tätig sind. Ihre „Signalstärke“ ist verschwindend klein, ein Empfänger für diese Wellen muss also sehr empfindlich sein. Er ist aber einfach aufzubauen – zumindest dann, wenn es, wie in meinem Fall, nur um den Nachweis der Schumann-Resonanzen geht. Das Foto zeigt einen Probe-Aufbau meines Empfängers und der Antenne. Der Ausgang des Empfängers ist einem PC verbunden, der die „Sendungen“ des Gewitterfunks aufzeichnet. Der zeitliche Verlauf des gespeicherten Signals ist ein Wechselstrom, der sich kaum vom Rauschen eines ohmschen Widerstandes unterscheidet. Mit Hilfe eines FFT-Programms (FFT = Fast Fourier Transform) kann man dennoch feststellen, welche Frequenzen in diesem Signal vorhanden sind und sogar messen, mit welcher relativen Stärke das der Fall ist. Das Diagramm zeigt das Ergebnis der Fourieranalyse: auf einem Untergrund von Rauschen mehrere breite „Buckel“ und zwei scharfe Linien bei 16,7 und 50 Hz. Die breiten Buckel bei 8, 14, 20, 26 und 32 Hz sind die Schumann-Resonanzen, die scharfen Linien entsprechen den Frequenzen des Bahnstroms (16,7 Hz) und der Energieversorgung (50 Hz). Ich gebe zu, die Resonanzen sind nicht sehr ausgeprägt – es ging nur um deren Nachweis, nicht um eine quantitative Messung. Hier mehr über dieses Experiment.

Und auch noch etwas Theorie: Man kann beispielsweise berechnen, bei welchen Frequenzen die Gewitter auf „Sendung“ sind. Die Rechnungen erfordern etwas Mathematik².

¹ W. O. Schumann war Professor für Physik und Direktor des Elektrophysikalischen Instituts der TU München.

² Die Rechnungen sind Näherungslösungen. Auch diese mathematisch aufwändigere Rechnung ist noch eine Näherung.

Radioastronomie für Anfänger (wie mich):

Richtet man eine Satellitenschüssel auf die Sonne, erhöht sich der Rauschpegel am Ausgang des Antennenkonverters (LNC, low noise converter) bezogen auf den Wert, den man normalerweise misst („normalerweise“ bedeutet zum Beispiel, dass die Antennenschüssel auf eine Himmelsregion fernab von der Sonne gerichtet wird). Ein Satellitenortungsgerät (Satfinder) zeigt diesen erhöhten Rauschpegel an. Das Foto zeigt die Messanordnung. Mit diesem „Experiment“ zeigt man, dass die Sonne nicht nur sichtbares Licht, sondern auch Radiostrahlung aussendet – im vorliegenden Experiment Radiostrahlung von ca. 10 GHz.  Die Intensität dieser Strahlung gibt man in der Regel an als die Temperatur eines schwarzen Körpers, der mit derselben Intensität strahlt. Durch Vergleich mit der Strahlung einer Hauswand o. ä. kann man die Temperatur der Sonne bei 10 GHz bestimmen. Es sind (11 ± 1) ∙ 10³ K (Kelvin). Dieser Wert fügt sich gut in das Diagramm ein, das in der Literatur für die Strahlungsstärke der ruhigen Sonne angegeben wird, siehe die nachfolgende Abbildung. In dieser Abbildung ist auch das Ergebnis einer Messung bei 4 GHz eingetragen, ausgeführt von Studenten im Physik-Praktikum einer Hochschule.

Der von mir bei 10 GHz gemessene Wert 11000 K ist größer als die Temperatur der Sonne im Bereich des sichtbaren Lichts, die 6000 K beträgt. Das deutet darauf hin, dass die Sonne nicht wie ein idealer schwarzer Körper strahlt. Mehr zu diesem Experiment.