Abb. 1 Abb. 2
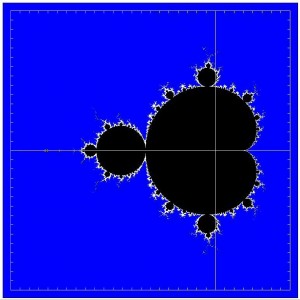
Nicht Neues, aber immer wieder interessant: Mandelbrots „Atlas“ der zusammenhängenden Julia-Mengen – genannt „Apfelmännchen“. Die Mandelbrotmenge ist das schwarz gefärbte Gebiet in Abbildung 1. Interessant ist vor allem der Rand der Mandelbrotmenge. Abbildung 2 zeigt ein Beispiel.
Zur Mathematik der Juliamengen und der Mandelbrotmenge.
Die Mandelbrot-Menge ist eine Menge komplexer Zahlen, die durch folgenden Rechenprozess entsteht: Betrachte den Term z2 + c, wobei z eine komplexe Zahl ist, die sich ändern darf (eine Variable), und c eine komplexe Zahl ist, deren Wert konstant bleibt. Starte mit der Zahl z0 = 0 + 0i und berechne den Wert des Terms z1 = z02 + c. Wegen z0 = 0 ist z1 = c. Setze diese Zahl erneut in den Term z2 + c ein. Das heißt, berechne z2 = z12 + c. Es ergibt sich z2 = c2 + c. Im nächsten Schritt erhält man z3 = z22 + c = (c2 + c)2 + c, usw. Es entsteht eine Folge von Zahlen z0, z1, z2, z3, … . Nennt man das Ergebnis nach dem n-ten Schritt zn, so ist die (n +1)-te Zahl zn+1 = zn2 + c. Da jede Zahl durch Rückgriff auf die vorherige berechnet wird, spricht man von einer rekursiv definierten Folge. Die wiederholte Anwendung der Rekursionsformel zn+1 = zn2 + c nennt man auch Iteration. Für c = 1 + i ergibt sich beispielsweise: z1 = 1 + i, z2 = 1 + 3i, z3 = –7 + 7i, z4 = 1 – 97i, usw. Man stellt fest, dass Real- und Imaginärteil von z im Verlauf der Iteration sowohl größer als auch kleiner werden und bisweilen das Vorzeichen wechseln. Interessant ist, wie weit sich z dabei vom Nullpunkt der komplexen Zahlenebene entfernen. Der Abstand einer komplexen Zahl z vom Nullpunkt heißt Betrag dieser Zahl und ist die Hypotenuse in einem rechtwinkligen Dreieck, dessen Katheten Real- und Imaginärteil sind. Daher gilt nach dem Satz von Pythagoras für den Betrag |z| = √(x2 + y2). Zur Mandelbrotmenge M gehören nun alle diejenigen komplexen Zahlen c, für die der Betrag von zn auch nach unendlich vielen Iterationsschritten nicht über alle Grenzen wächst. Das heißt, diejenigen Zahlen c, für die der Abstand von Nullpunkt der Folgeglieder zn eine (geeignet gesetzte) Grenze nicht überschreitet. Trägt man diese Werte von c in die komplexe Zahlenebenen ein, ergibt sich ein zusammenhängendes Gebiet, das die Form eines liegenden „Apfelmännchens“ hat.
Der Rand diese Gebiets ist ungeheuer formenreich: es gibt Kreise, Spiralen, Schnecken, alle haarfein verästelt und zum Teil in sich verschlungen. Erstaunlich ist, dass der Rand auch bei noch so starker Vergrößerung nie glatt wird. Er ist, wie man sagt, ein Fraktal. In dem Bereich der Zahlenebene, in dem sich die Werte von c befinden, für die zn über alle Grenzen wächst, zählt man die Anzahl der Iterationen, die bis zum Überschreiten einer (geeignet gesetzten) Grenze benötigt werden. Punkte gleicher Iterationszahl verbindet man miteinander. Auf diese Weise entstehen Linien gleicher „Fluchtgeschwindigkeit“. Der Ausschnitt Abb. 2 entspricht dem Intervall [– 0.95; – 0.88333] für den Realteil von c, und dem Intervall [– 0.3; – 0.233333] für den Imaginärteil von c.