Kategorie: Physik als Hobby

Der Versuch zum Fotoeffekt, ein Highlight der Schulphysik, hat einen Nachteil: Er liefert einen zu kleinen Wert für die Plancksche Konstante. Jedenfalls ist das meine Erfahrung¹. Versuchsprotokolle von Studenten, die das Experiment im physikalischen Praktikum an einer Hochschule ausführen mussten, bestätigen das². Ein Teil dieser Experimente benutzt die so genannte Gegenfeldmethode³. Bei ihr ist die Bestimmung der Fotostrom-Nullstelle kritisch. Eine theoretische Berechnung der Fotostromkurve und das daraus abgeleitete Verfahren, auf den Wert Null des  Fotostroms zu extrapolieren, liefert aber offenbar keine Verbesserung⁴. Auch die vielfach angewandte Auflademethode⁵ ergibt kaum „bessere“ Werte der Planckschen Konstanten.

Gründe für die Diskrepanz zwischen Theorie und Experiment werden in der Literatur diskutiert⁶, aber nur zum Teil experimentell untersucht. Genannt werden u. a. nicht exakt monochrome Beleuchtung, Streulicht, das nicht genügend unterdrückt wird, Niederschlag von Kathodenmaterial auf der Anode, falsche Extrapolation auf den Wert Null des Fotostroms, ein zu kleiner Isolationswiderstand zwischen Kathode und Anode und die Tatsache, dass auch Elektronen oberhalb der Fermikante zum Fotostrom beitragen und so die Maximalenergie der Fotoelektronen bzw. die Aufladespannung verändern.

Ich schließe daraus: Das Experiment ist mit einem systematischen Fehler behaftet, dessen Ursache bisher unbekannt ist. Vielleicht nur mir unbekannt. Jedenfalls warte ich immer noch auf einen Versuch zum Fotoeffekt (überzeugend protokolliert und mit realistischer Fehlerabschätzung), dessen Wert die Plancksche Konstante innerhalb der Fehlergrenzen reproduziert.

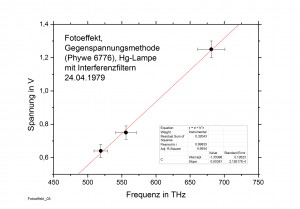
Das Diagramm ist das Ergebnis einer meiner Messungen nach der Gegenfeldmethode. Es zeigt die Gegenspannung, bei der der Fotostrom Null wird, aufgetragen als Funktion der Frequenz der Strahlung. Die Steigung der Geraden ist gleich der Planckschen Konstanten dividiert durch die Elementarladung. Passt man eine Gerade an die Messpunkte an, erhält man h/e =  (3,81 ± 0,22)·10^-15 eVs  oder   h = (6,10 ± 0,35)·10^-34 Js. Der Literaturwert ist  h = 6,63·10^-34 Js.

¹   Eine grobe Beschreibung der Physik des Versuchs und eigene Resultate hier.
²   KIT, Musterprotokolle, in www-ekp.physik.uni-karlsruhe.de/~simonis/praktikum/…/musterprotokolle.
³   Gegenfeldmethode siehe ¹.
⁴   Hübel, H. H., in http://www.forphys.de/Website/qm/schulversuche/fotschul.html
⁵   Auflademethode siehe ¹.
⁶    z. B. Hübel, H. H., a. a. O.
 

Kann man Physik „verstehen“? Im Studium habe ich Physik gelernt, aber nicht verstanden. Die Erfahrung, dass man Physik auch verstehen kann, kam später. Und wurde durch ein Buch ausgelöst: Concepts in Physics von R. Adair¹. Es ist wenig bekannt – vermutlich, weil es sich nicht zum Pauken für die Prüfung eignet. Das Buch liefert nicht nur die Physik eines Phänomens, sondern stellt auch immer den Zusammenhang her mit der dahinter liegenden Theorie². Ein Beispiel: Das Magnetfeld eines stromführenden Drahtes. Es führt zu einer Kraft auf eine bewegte Ladung. Betrachtet man es von einem Koordinatensystem aus, das sich relativ zum Draht bewegt und in dem die Ladung ruht, ist es ein elektrisches Feld. Im Laborsystem wird daraus ein Magnetfeld. Kein Problem, sagt der Physiker, das erklärt die Relativitätstheorie unter dem Stichwort Lorentztransformation  und fängt an zu rechnen.  Adair‘s Buch zeigt, wie man dies „verstehen“ kann: Der Draht ist im mitbewegten System wegen der unterschiedlichen Lorentzkontraktion der Atomrümpfe und Elektronen elektrisch geladen und übt deshalb eine elektrische Kraft auf Ladungen aus. Nach der Rücktransformation ins Laborsystem erscheint diese als magnetische Kraft. Ich habe das Thema mehrmals im (Schul-) Unterricht behandelt, auch das Experiment dazu vorgeführt. Die Rechnungen sind nicht einfach; ich hoffe, meine Schüler/innen haben sie trotzdem „verstanden“.

Das Foto zeigt die Anordnung des Experiments: Ein Elektronenstrahl wird im Magnetfeld des stromführenden Drahts abgelenkt. Der Draht verläuft oberhalb des Glaskolbens parallel zur Strahlachse und ist als schwach roter Stab erkennbar. Der Strahl hinterlässt auf dem Schirm im Kolben die bläulich-weiße Leuchtspur.

¹  Robert K. Adair: Concepts in Physics, Academic Press, New York NY, 1969. Natürlich bemühen sich alle Physiklehrbücher, die Physik verständlich zu machen. Hier eine Liste der Bücher,  in die ich bei Bedarf hineinschaue.

²  Im Vorwort des Buchs wird dieser Zusammenhang genannt „ … the intenal importance and internal consistency of physics …“.  Adair weiter unten: „In particular, I have attempted to give the student a reasonably sophisticated understanding of quantum mechanics, the special and general theories of relativity, and the importance of classifying the symmetries which we seem to observe in the universe.“

Beim Stöbern im Internet gerate ich hin und wieder auf Sites, in denen es um Schulphysik geht (kein Zufall, in dieser Branche habe ich früher gearbeitet). Zum Beispiel auf die Site einer Lehrmittelfirma. Dort wird ein Experiment beschrieben, das die Hallkonstante von Kupfer misst¹ – und das mit einer Genauigkeit von ± 1%. Erstaunlich. Da kommen Neugier und Neid auf, so genau hatte ich diese Größe nicht gemessen. Ich kramte meine früheren Aufzeichnungen heraus: ± 30% war mein Messfehler damals. Hier mein (überarbeitetes) Messprotokoll.

Was den Wert der Konstanten angeht, konnte ich den Literaturwert innerhalb meiner ± 30% Fehlergrenzen bestätigen. Doch der Wert selbst war falsch. Dass ein „falscher“ Wert trotzdem richtig sein kann, muss man im Unterricht begründen. In der Schulphysik herrscht die Meinung, ein (Demonstrations-) Experiment tauge nichts, wenn es nicht den „richtigen“ Wert liefert. Das stimmt natürlich nicht, jede Messung  ist ungenau. Man schätzt die Ungenauigkeit ab und gibt sie zusammen mit dem Messwert als „Messfehler“ an, in der Regel hinter dem Zeichen „±“. Beispiel: Die damals von mir bestimmte Hallkonstanten R_H  = – (5,0 ± 1,6) ·10 ^{– 11} m³/As.

Im Übrigen ist das Wort „Fehler“ irreführend. Es suggeriert, man habe die „Scheibe“ nicht getroffen – falsch. Der Fehler ist nichts anderes als (ein Schätzwert für) die Größe der Scheibe, die man bei wiederholten Versuchen mit einer Wahrscheinlichkeit von beispielsweise 68% (1σ-Wert) trifft.

Das Foto zeigt einen Teil meines Versuchsaufbaus. Vielleicht ist von Interesse, was das Experiment für die Physik hergibt: Aus dem genannten Wert von R_H folgt, dass in metallischem Kupfer ein Atom im Mittel 1,5  Elektronen für die Stromleitung zur Verfügung stellt.

¹ Versuchsbeschreibung der Fa. Phywe: https://www.phywe.de/de/hall-effekt-in-metallen.html#tabs3

Auch der Umweg führt zum Ziel –  wenn er kein Abweg ist. Einmal angekommen, kann man behaupten, man hätte den direkten Weg genommen. Das kann eine Welle nicht. Sie kommt nämlich, da der Umweg länger als der direkte Weg ist, mit einer anderen Phase am Ziel an als die direkte Welle. Voraussetzung ist, dass beide Wellen zur gleichen Zeit und mit der gleichen Anfangsphase starten. Die Phasendifferenz zwischen Umweg- und direkter Welle drückt man üblicherweise als Winkel zwischen 0° und 360° aus (zwischen 0 und 2π, wenn man im Bogenmaß rechnet). Ist sie 2π oder ein Vielfaches davon, sind beide Wellen im Takt und verstärken sich. Sie können sich aber auch auslöschen. In diesem Fall ist die Phasendifferenz nur halb so groß (π oder ein Vielfaches davon). Dann treffen am Ziel Wellenberg und Wellental aufeinander. Je nach Längendifferenz zwischen direktem und Umweg beobachtet man dort, wo die Wege wieder zusammentreffen, auch Werte zwischen maximaler und minimaler Schallintensität. Aus dem Verlauf des Schallpegels als Funktion der Weglängendifferenz lässt sich die Schallgeschwindigkeit bestimmen. Hier Messungen dazu. Das Foto zeigt die Messapparatur.

… gibt es nicht nur als Klangkörper in Orgeln. Auch unsere Schule besitzt eine solche Pfeife. Gedackt heißt ja bekanntlich, dass ein Ende des Pfeifenrohrs geschlossen, das andere offen ist. Die Pfeife unserer Physiksammlung ist ein Glasrohr, dessen geschlossenes Ende aus einem Kolben besteht. Der ist verschiebbar, so dass die Länge der Luftsäule, die sich im Rohr befindet, variiert werden kann. Die Luftsäule wird durch Schallwellen aus einem Lautsprecher in Schwingungen versetzt, der sich vor dem offenen Ende befindet. Speist man den Lautsprecher mit einem Sinus-Ton fester Frequenz und schiebt dabei den Kolben hin und her, schwingt die Luftsäule bei bestimmten Kolbenpositionen besonders heftig. Resonanz heißt das Phänomen – wir kennen es: ohne Resonanz keine Opernarien in der Duschkabine.
Bei geeigneter Frequenz treten Resonanzen in unserer gedackten Pfeife bei mehreren Kolbenpositionen auf. Aus deren räumlichem Abstand bestimmen wir die Schallgeschwindigkeit in Luft. Das Foto zeigt den Versuchsaufbau mit Tongenerator (gelbes Gehäuse im Hintergrund), Lautsprecher, Glasrohr mit Kolben (verdeckt durch einen Messstreifen) und Schall-Pegelmesser (vorne rechts). Mehr ….

Eine Aufgabe aus dem Bundeswettbewerb Physik 2005 (Sekundarstufe 1)¹: Die Nachwuchsphysikerin Josefine soll ihr Auge, durch eine Sammellinse vergrößert, in einem Spiegel betrachten. Sie findet zwei verschiedene Möglichkeiten, ihr eigenes Auge vergrößert zu sehen – einmal als aufrecht stehendes, das andere Mal als umgekehrtes Bild. Für beide Fälle soll sie den Strahlengang konstruieren.

Einfache Sache, denkt der Profi. Einige Linsen und ein Spiegel sind schnell beschafft, dann beginnt das Herumprobieren. Das führt zu nichts, weil er keinen Plan hat. Er konstruiert aufs Geratewohl einige Strahlengänge. Auch das verschafft nicht die nötige Übersicht. Also muss etwas Theorie her. Dabei ergibt sich die Frage, wie man die Vergrößerung definiert. Zumindest dann, wenn man die Linse als Lupe benutzt.

Beim Experimentieren, jetzt etwas systematischer, stellt sich heraus, dass man sich beschränken sollte. Nämlich auf die Betrachtung mit entspanntem (auf Unendlich eingestelltem) Auge. Anderenfalls ist es schwierig, Experiment und Theorie zu vergleichen. Hier ein kleiner Beitrag zu diesem Problem.

Die Bildgröße B_S ist abhängig davon, wie weit das Auge von der Linse entfernt ist (y) und welchen Abstand der Spiegel von der Linse hat (x). Die Abbildung ist eine 3D-Darstellung der Funktion B_S(x, y). Mit entspanntem Auge beobachtet man in der Nähe der steilen „Wände“, das sind die Polstellen bzw. Polkurven von B_S.

¹  MNU-Zeitschrift 58/6 (1.9.2005)

Faust windet sich, als Gretchen ihn nach seiner Religion fragt. Kann man verstehen. Aber den Schall zur Begründung seiner Ausflüchte  heranzuziehen, ist ein Missgriff, den wir Physiker ihm nicht verzeihen. Immerhin ist die Lehre vom Schall, in der Branche Akustik genannt, ein wichtiges Gebiet der Physik. Denn der Schall macht überall dort, wo er sich ausbreitet, die Welle – in der Luft, im Wasser, im Festkörper, im Nierensteinzertrümmerer (als Stoßwelle) und wer weiß wo.

Hier geht es um die Welle in der Luft – genauer gesagt, um mehrere  Wellen. In unserem Fall werden sie von zwei Lautsprechern abgestrahlt und überlagern sich. Sie interferieren, wie man sagt. Dabei verstärken sie sich oder löschen sich gegenseitg aus. Das Foto zeigt eine Messanordnung, mit der man die Interferenz von Schallwellen in Luft zeigt. Mehr davon hier.

… kann es recht gut, soll es aber nicht. Es soll sich genau auf der Grenze zwischen Kriechen und Schwingen bewegen – nämlich im aperiodischen Grenzfall. Die Rede ist vom Galvanometer, einem physikalischen Messinstrument für kleine Stromstärken (Mikro-Ampere). Im aperiodischen Grenzfall bewegt sich sein Zeiger in der kürzest möglichen Zeit auf den Messwert zu.

Der Physiker kennt das Galvanometer aus dem physikalischen Grundpraktikum. Bei uns Studenten galt der Versuch als hardcore physics. Uns fehlte die Mathematik dazu (die wurde erst in höheren Semesetern serviert) und meist auch die Zeit für die Vorbereitung.

Das Instrument ist ein Fossil aus dem analogen Zeitalter. Ich entdeckte ein Exemplar kürzlich in der Sammlung meiner ehemaligen Arbeitsstätte. Es funktionierte noch, ich habe es geprüft. Hier das Ergebnis. Auch die Bewegungsgleichung des Torsionszeigers habe ich mir noch einmal angesehen: Er kriecht und schwingt tatsächlich.

Noch ein Beitrag zum Thema Regenbogen:

Wir stehen mit dem Rücken zur Sonne und vor uns regnet es. Am Himmel sehen wir einen Regenbogen. Muss der immer am Himmel stehen? Das Foto zeigt: Er kann sich auch tief unten in den Grand Canyon verkriechen. Physik und Geometrie erklären das. Wer es genauer wissen will, muss noch einmal zur Schule – in den Physikunterricht:

Es ist gegen Mittag und die Sonne steht hoch am Himmel – das ist im Sommer in Arizona so üblich. Wir denken uns die Gerade, die die Sonne mit unserem eigenen Standort verbindet, und verlängern sie in der Richtung, in die wir blicken. Sie trifft, wo immer wir sie enden lassen wollen, auf einen imaginären Punkt, den Sonnengegenpunkt (engl. antisolar point). Der liegt schon ziemlich tief im Canyon. Die Gerade ist die Achse eines Kegels mit dem Öffnungswinkel 42°. Unter diesen Winkel relativ zur Kegelachse (oder relativ zum Sonnengegenpunkt) erscheint der Bogen. Warum immer 42°, egal wie und wann wir ihn sehen? Das ist eine Frage an die Physik. Die sagt, dass wir nur einen einzelnen Wassertropfen betrachten brauchen, um den Regenbogen zu verstehen. Ein Sonnenstrahl wird beim Eintritt in ihn gebrochen, im Innern reflektiert, und am Austritt wiederum gebrochen. Wie, das sagen uns Brechungs- und Reflexionsgesetz. Rechnen wir alles unter Beachtung dieser Gesetze durch, erhalten wir den genannten Öffnungswinkel 42°. Aber nur für eine der Farben, die im Sonnenlicht vertreten sind. Ist z. B. Rot die Farbe, die unter 42° erscheint (der genaue Winkel hängt etwas von der Tropfengröße ab), sieht man das Violett am anderen Rand des Bogens unter einem etwa 2° kleineren Winkel.

Wenn der Sonnengegenpunkt schon sehr tief unter uns liegt, wie hier bei hochstehender Sonne, hat der Kegelmantel (Regenbogen) bei einem Öffnungswinkel von 42° keine Chance, über den Horizont heraus zu ragen und sich am Himmel auszubreiten. Allerdings muss es tief unter uns, wie hier im Canyon, auch regnen.

Theoretische Überlegungen zum Regenbogen gibt es seit dem Mittelalter. Einen Überblick bis zu den Arbeiten des 19. Jahrhunderts (Airy ) liefert J. D. Jackson: From Alexander of Aphrodisias to Young and Airy, Physics Reports 320 (1999), 27 – 36. Ich habe zu diesem Artikel Notizen gemacht: Bemerkungen, Neben- und Zwischenrechnungen, um ihn für mich verständlich zu machen. Mein Regenbogen-Modellexperiment mit einem Acrylglaszylinder statt Wassertropfen ist vielleicht auch von Interesse.