Dezember 2013

Weihnachtslied und 2-Quadrate-Satz

23. Dezember 2013 in Computergrafik

Zum Gitterpunktsatz

Pierre de Fermat entdeckte, dass Primzahlen größer als 2 sich genau dann in eine Summe aus zwei Quadraten zerlegen lassen, wenn sie sich in der Form 4n + 1 (n ∈ N ) darstellen lassen – oder, als Satz formuliert: Eine Primzahl p größer als 2 lässt sich dann und nur dann in eine Summe aus zwei Quadratzahlen zerlegen, wenn sie bei der Division durch 4 den Rest 1 lässt, wenn also gilt p ≡ 1 (mod 4). Beispiele: 5 = 1²+ 2² oder 13 = 2²+ 3². Der Satz ist unter dem Namen Zwei-Quadrate-Satz in die Geschichte der Zahlentheorie eingegangen und, wie man liest, eines der Highlights dieser Disziplin. Ian Stewart hat den Beweis dieses Satzes in eine humorvolle „Nacherzählung“ von Charles Dickens „Ein Weihnachtslied in Prosa“ (A Christmas Carol in Prose) eingebettet¹.

Er greift dabei, wie vielfach üblich, auf einen weiteren berühmten Satz der Mathematik zurück, den Minkowskischen Gitterpunktsatz. Der ist an Anschaulichkeit nicht zu übertreffen und verlangt geradezu danach, computergrafisch dargestellt zu werden. Ich konnte nicht widerstehen und habe einige Computerzeichnungen in Anlehnung an den Artikel von Stewart programmiert. Die Abbildung zeigt ein Beispiel.

Bäume: Zeichnungen und Aquarelle

17. Dezember 2013 in Malerisches

Nach den Fotos der Baumallee Bassenheim jetzt eine kleine Galerie mit Zeichnungen und Aquarellen, die Bäume, Baumgruppen und Alleen zeigen – angeregt durch die Formen der Bassenheimer Alleebäume.

Goldener Schnitt und Impedanz

14. Dezember 2013 in Physik als Hobby

Ein „goldenes“ Rechteck

Impedanz ist ein anderes Wort für Wechselstromwiderstand. Es geht also um Elektrotechnik. Um einen Stromkreis, dessen Impedanz von der Frequenz der Stromquelle abhängt. Die Einzelheiten später.

Zunächst zum Goldenen Schnitt: Wir zeichnen ein Rechteck, dessen Länge sich zur Breite verhält wie (√5 + 1)/2 zu 1, oder näherungsweise wie 1,618 zu 1. Spaltet man das größte Quadrat ab, das hineinpasst, bleibt ein Rechteck übrig mit demselben Seitenverhältnis. Aus diesem entfernt man wiederum das größte einbeschriebene Quadrat, und wiederum bleibt ein Rechteck übrig, dessen Seitenlängen sich wie (√5 + 1)/2 zu 1 verhalten. Das Spiel lässt sich ad infinitum fortsetzen – aber nur dann, wenn man wie oben mit dem genannten Seitenverhältnis beginnt. In der Abbildung sind die ersten Schritte erkennbar. Die Zahlen (√5 + 1)/2 = 1,618339… und (√5 – 1)/2 = 0,618339… , die hier eine Rolle spielen, sind die Teilungsverhältnisse des Goldenen Schnitts. In der Kunst soll er besonders angenehme Proportionen erzeugen. Dass er auch in anderen Bereichen „mitmischt“, ist bekannt.

Ein Beispiel aus der Elektrotechnik ist der nachfolgende Wechselstromkreis. Seine Impedanz

Stromlaufplan unserer Schaltung

(sein Wechselstromwiderstand) ist Null für zwei Kreisfrequenzen, die durch die Resonanzfrequenz 1/√LC der Einzelkreise im Verhältnis des Goldenen Schnitts geteilt wird. Mehr

Schreibtischexperiment: c nach Römer

1. Dezember 2013 in Physik als Hobby

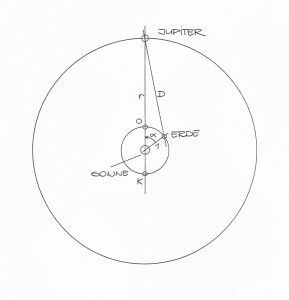
Abbildung: Bahnen von Erde und Jupiter und Bestimmung der Entfernung Jupiter-Erde. O: Jupiter in Opposition zur Sonne (nachts), K: Jupiter in Konjunktion zur Sonne (am Tage). Entfernungen in astronomischer Einheit AE (1 AE = 149,6 Millionen km)

Ein geniales „Experiment“, am Schreibtisch nachempfunden: Ole Rømers Bestimmung der Lichtgeschwindigkeit.

Zuvor einige Erläuterungen zu Messmethode: Schon Galilei richtete nachts sein Fernrohr auf den Planeten Jupiter und stellte fest, das dieser von Monden umkreist wird. Damit waren Jupiter und seine Monde das erste System, an dem man durch Beobachtung von „Außen“ die Bewegung von Satelliten studieren konnte. Ole Rømer untersuchte das Kreisen der Jupitermonde genauer. Und prompt entdeckte er, dass einer der Monde, nämlich Io, es mit den Gesetzen der Physik offenbar nicht so genau hielt: Seine beobachtete Umlaufzeit wurde größer, je weiter sich die Erde vom Jupiter und damit von ihm, dem Mond Io, entfernte. Wie kommt es dazu?

Die (synodische) Umlaufzeit des Jupitermondes Io beträgt T_Io = 1,76986 Tage (d). Dies ist die Zeitspanne, die beispielsweise verstreicht zwischen zwei aufeinanderfolgenden Austritten dieses Mondes aus dem Kernschatten des Jupiters (Verfinsterungsende). Rømer bestimmte die Zeitpunkte der Verfinsterungsenden über längere Zeit hinweg. Um seine Vorgehensweise nachzuvollziehen, nehmen wir an, dass Jupiter am Anfang seiner Beobachtungsreihe in Opposition zur Sonne stand. Die Erde befindet sich dabei im Punkt O der Abbildung, so dass die Entfernung zwischen Jupiter und Erde minimal war. In der Folgezeit nahm der Abstand zwischen Erde und Jupiter fortlaufend zu, da sich die Erde in Richtung Konjunktionsstellung (Punkt K in der Abbildung) bewegte, während Jupiter wegen seiner 12-jährigen Umlaufzeit praktisch auf der Stelle trat. Rømer stellte fest, dass die Verfinsterungsenden im Laufe der Zeit immer später eintrafen als vorherberechnet. Das heißt, das Verfinsterungsende nach beispielsweise 90 Io-Umläufen trat nicht genau 90 ×1,76986 Tage später ein als das erste von ihm beobachtete Verfinsterungsende, sondern hinkte einige Minuten hinterher. Er zog daraus den richtigen Schluss, dass diese Verzögerung der Zeitdauer entspricht, die das Licht benötigt, um die Entfernungsdifferenz zwischen den Positionen der Erde am Anfang und Ende der Beobachtungsreihe zurückzulegen.

Verzögerung und Entfernungsdifferenz lassen sich aus Ephemeridentabellen bzw. astronomischen Tafelwerken ermitteln. Die Rechnung ergibt beispielsweise, dass für eine Entfernungsdifferenz von 150,1 Millionen Kilometern die Verzögerung 9,28 Minuten = 557,1 Sekunden beträgt. Daraus folgt für die Lichtgeschwindigkeit ein Wert von c = 269500 km/s. Nimmt man an, dass die Verzögerung auf etwa ± 2 Minuten genau bestimmt werden kann, ergibt sich für die Lichtgeschwindigkeit einschließlich Fehler c = (269500 ± 58100) km/s. Dieser Wert ist innerhalb der Fehlergrenzen mit dem Literaturwert c = 299792,458 km/s verträglich.