Pierre de Fermat entdeckte, dass Primzahlen größer als 2 sich genau dann in eine Summe aus zwei Quadraten zerlegen lassen, wenn sie sich in der Form 4n + 1 (n ∈ N ) darstellen lassen – oder, als Satz formuliert: Eine Primzahl p größer als 2 lässt sich dann und nur dann in eine Summe aus zwei Quadratzahlen zerlegen, wenn sie bei der Division durch 4 den Rest 1 lässt, wenn also gilt p ≡ 1 (mod 4). Beispiele: 5 = 12+ 22 oder 13 = 22+ 32. Der Satz ist unter dem Namen Zwei-Quadrate-Satz in die Geschichte der Zahlentheorie eingegangen und, wie man liest, eines der Highlights dieser Disziplin. Ian Stewart hat den Beweis dieses Satzes in eine humorvolle „Nacherzählung“ von Charles Dickens „Ein Weihnachtslied in Prosa“ (A Christmas Carol in Prose) eingebettet1.
Er greift dabei, wie vielfach üblich, auf einen weiteren berühmten Satz der Mathematik zurück, den Minkowskischen Gitterpunktsatz. Der ist an Anschaulichkeit nicht zu übertreffen und verlangt geradezu danach, computergrafisch dargestellt zu werden. Ich konnte nicht widerstehen und habe einige Computerzeichnungen in Anlehnung an den Artikel von Stewart programmiert. Die Abbildung zeigt ein Beispiel.
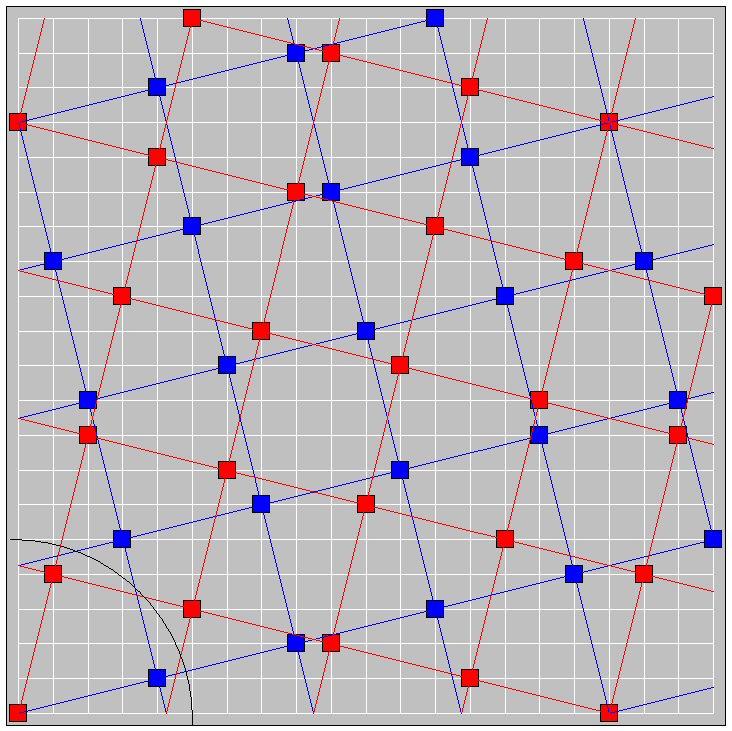
Der Gitterpunktsatz lautet: Sei L = {(x, y)∈ Z2} ein Gitter in der xy-Ebene. Ist G ∈ R2 ein konvexes Gebiet, das symmetrisch zum Ursprung (0, 0) liegt und dessen Flächeninhalt mindestens das Vierfache der Fläche einer Gittermasche beträgt, dann liegt innerhalb von G mindestens ein weiterer Punkt (x, y) des Gitters L. Die Abbildung zeigt ein Beispiel: Die roten und blauen Karos bilden je ein Gitter, für deren Gitterpunkte (x, y) der Term x2 + y2 ein Vielfaches der Primzahl 17 ist. Im Fall des roten Karos (5,3) beispielsweise ist x2 + y2 = 52 + 32 = 34 = 2·17. Der Flächeninhalt einer Masche des Gitters beträgt, wie man leicht nachzählt, 17 Einheits-Kästchen. Der Kreis um den Ursprung in der linken unteren Ecke hat den Radius 5, sein Flächeninhalt ist also 25π – das ist näherungsweise 78,53. Er ist damit größer als das Vierfache der Maschenfläche des Gitters: 4·17 = 68. Nach dem Gitterpunktsatz von Minkowski gibt es dann mindestens einen vom Ursprung verschiedenen Gitterpunkt, der innerhalb des Kreises liegt. Im ersten Quadranten sind es aus Symmetriegründen sogar zwei Punkte (siehe Abbildung).
Hier ist meine Nacherzählung der Nacherzählung von Stewart.
1 Ian Stewart: „Ein Weihnachtslied in Prosa“, Spektrum der Wissenschaft – Digest: Mathematische Unterhaltungen (2002?)