Monat: Januar 2016

Van Gogh’s Sternennacht im PC

 in Malerisches, Physik als Hobby

Sternennacht_Vergl_Himmelsansicht_03Schon zu Zeiten der ersten PC’s entstanden Computerprogramme, die Himmelsansichten für einen beliebigen Ort der Erde und zu beliebigen Zeiten berechneten. Ich benutzte sie u. a. im Astronomieunterricht der Schule. Damit konnten meine Schüler(innen) beispielsweise die große Konjunktion von Jupiter und Saturn um das Jahr 7 v. Chr. (Stern von Bethlehem?) am Bildschirm verfolgen.

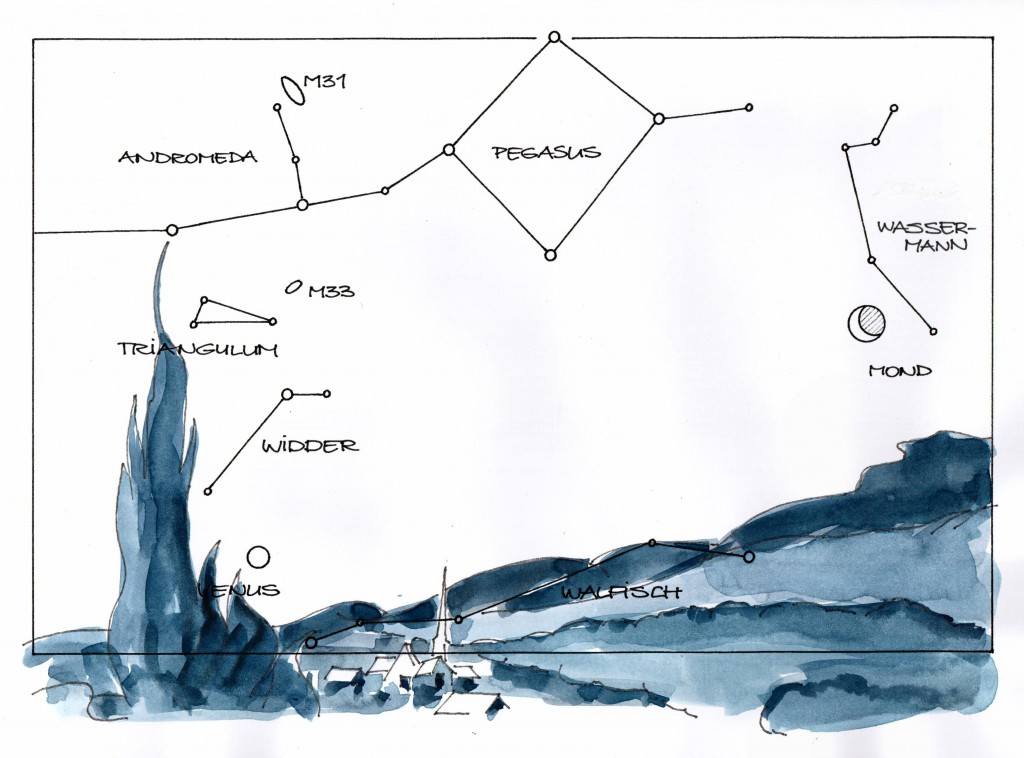
Etwa zur selben Zeit fiel mir ein Buch  in die Hand mit dem Titel „Vincent van Gogh – Die Sternennacht“. Darin zeigt der Kunsthistoriker A. Boime ¹, dass van Gogh’s  berühmtes Gemälde eine durchaus realistische Ansicht des Nachthimmels darstellt – nämlich den Anblick, der sich dem Künstler bot, als er das Bild malte. Ort und Zeit kann man den Lebensdaten van Gogh’s und seinen Briefen an den Bruder Theo  entnehmen: Das Bild entstand in St. Remy-de-Provence  etwa am 19. Juni 1889 gegen 3 Uhr morgens. Boime benutzte seinerzeit Daten eines Planetariums, um den Himmel über dem südfranzösischen Ort zu diesem Zeitpunkt darzustellen. Es zeigte sich, dass van Gogh den Mond  genau dort platzierte, wo er den astronomischen Berechnungen nach am Himmel stehen sollte, und dass der helle Stern rechts neben der großen Zypresse mit großer Sicherheit den Planeten Venus darstellt. Im Übrigen waren neben A. Boime auch andere² in dieser Sache professionell tätig (und sind es immer noch).

Da sich Boime’s Planetarium, MS-DOS sei Dank, durch die erwähnte Software ersetzen ließ, konnte ich seine Entdeckung am eigenen PC nachvollziehen – eine leichte Übung für das benutzte Redshift-Programm. Das Bild ist eine Nachzeichnung des Computerdisplays, von mir ergänzt durch eine Skizze der Landschaft mit Dorf und Zypresse. Wie erwartet, bestätigte Redshift die „planetarisch“ erzeugte Darstellung.

Nach diesem (bescheidenen) Erfolg nahm ich mir weitere „Himmels“-Gemälde van Gogh’s  vor, verglich Leinwand- und Bildschirmdarstellung. Diese eher laienhaften Studien habe ich in einem kleinen Aufsatz zusammengefasst und daraus ein Beispiel für eine Facharbeit in der Oberstufe gemacht – eine fächerübergreifende Facharbeit³ in den Disziplinen Kunst und Physik bzw. Astronomie. Hier ist sie.

¹ Boime, A., Vincent van Gogh – Die Sternennacht, Frankfurt am Main 1989 (Fischer Taschenbuch Nr. 11237), z. Zt. ergriffen
² z. B. Olson, D., R. Doescher, Sky and Telescope, October 1988, S. 406, und Withney, C. A., Physics Today August 1992, 13 (1992)
³ ein Oxymoron?

Zentralprojektion zur MS-DOS-Zeit

 in Malerisches

Trinita_Masaccio_3_AugpunkteDas Stichwort Zentralperspektive erinnert mich an Computerspielereien aus dem MS-DOS-Zeitalter – Programme zur Zentralprojektion zu schreiben und damit „realistische“ 3D-Bilder zu erzeugen. Sehr realistisch waren die Bilder nicht, sie sind eher von sentimentalem Wert.  Anlass war eine Studienfahrt nach Florenz. Meine Schüler und Schülerinnen mussten zur Vorbereitung Referate über die Bedeutung und die Sehenswürdigkeiten der Stadt ausarbeiten und vortragen – unter anderem über Masaccios Trinitätsfresko in der Kirche Santa Maria Novella. Genauer gesagt, über die zentralperspektivische Darstellung in diesem Gemälde. Masaccios Gnadenstuhl-Fresko ist ja bekanntlich das erste Bild, in dem die Regeln der Zentralprojektion korrekt angewandt wurden. Ich fand das Thema interessant. Hier mein Beitrag dazu:

Read more

Fluchtpunkte

 in Malerisches

Drei Mal eine Zentralperspektive mit genau einem Fluchtpunkt – Aquarellstift-Zeichnungen:
(1) Renaissance-Park Valsanzibio (Italien), (2) Arches Natl. Park, Utah (USA),
(3) Park Avenue, New York City (USA)

ValsanzibioArches_Natl_Park Park_Ave_NYC

Reflexion vom Nagelbrett

 in Physik als Hobby

BraggReflexionCmWellen.foto2Ein Brett mit Eisennägeln, kein Uecker: Das Foto zeigt den Aufbau eines Physikexperiments – die Streuung von Hochfrequenzwellen an einem Kristall-Modell. Modell deswegen, weil der Versuch in der professionellen Physik an einem (optischen) Kristall mit Lichtwellen ausgeführt wird. Dort ist er mit dem Namen Bragg-Reflexion verknüpft. In der Schule benutzte ich die Modellversion mehrmals als Thema für Abiturklausuren (damals, als es noch kein Zentralabitur gab). Die Experimente dazu standen unter Zeitdruck: meist kam man erst in den Winterferien dazu, über Abiturthemen nachzudenken und die dazu passenden Experimente auszutüfteln. Am Ende der Ferien mussten die die Experimente funktionieren und die Aufgabenvorschläge fertig sein. An das hektische Experimentieren im ungeheizten Schulgebäude (in den Ferien) erinnere ich mich noch. Die Messdaten schlummerten seitdem in meinen Protokollbüchern. Ich habe sie jetzt noch ein Mal hervorgeholt und in Ruhe ausgewertet. Hier sind die Resultate.

2016 – pseudovollkommen und hexagonal

 in Verschiedenes

2016_mit_Schlingpflanzen_01Was hat das Jahr 2016 zu bieten – ich meine in mathematischer Hinsicht? Viel habe ich nicht entdeckt – aber auch nicht sehr eifrig nachgeforscht. Immerhin hat 2016 eine stattliche Anzahl von Teilern. Es sind genau 36, nämlich 1, 2, 3, 4, 6, 7, 8, 9, 12, 14, 16, 18, 21, 24, 28, 32, 36, 42, 48, 56, 63, 72, 84, 96, 112, 126, 144, 168, 224, 252, 288, 336, 504, 672, 1008 und 2016. Streicht man aus dieser Liste die Zahl 2016, bleiben die echten Teiler. Damit lässt sich etwas anfangen: Bildet man die Summe aus den echten Teilern 336, 672 und 1008, erhält man 2016. Auch andere Summen von (echten) Teilern ergeben 2016, z. B. 84 + 252 + 672 + 1008 = 2016. Zahlen, die sich als Summe einiger verschiedener echter Teiler schreiben lassen, heißen pseudovollkommen. Also ist das neue Jahr zwar nicht ganz vollkommen, aber immerhin pseudovollkommen (Vollkommen heißen die Zahlen, die gleich der Summe aller ihrer echten Teiler sind, Beispiel 6 = 1 + 2 + 3). Auf seine Pseudovollkommenheit kann sich 2016 aber nicht viel einbilden: Es ist nämlich durch 6 teilbar – und ein (fast trivialer) Satz der Mathematik besagt, dass alle durch 6 teilbaren Zahlen pseudovollkommen sind. Beweis: Jede Zahl von der Form 6k mit k = 1, 2, 3, … lässt sich schreiben als 6k = k + 2k + 3k, so dass jeder der Summanden 6k teilt. In unserem Fall ist k = 336. Also gilt 2016 = 6·336 = 336 + 2·336 + 3·336 =  336 + 672 + 1008. Das ist die oben genannte Zerlegung.

Interessant ist noch, dass 2016 eine Sechseckzahl (Hexagonalzahl) ist. Hexagonalzahlen erhält man, indem man eine Reihe Steine zur Hand nimmt und wie folgt anordnet: Man startet mit einem Stein, legt weitere 5 Steine so an, dass ein Sechseck mit der Seitenlänge von 2 Steinen entsteht. Dann verlängert man zwei benachbarte Seiten um je einen Stein und fügt weitere 7 Steine so hinzu, dass ein größeres Sechseck mit der Seitenlänge von 3 Steinen entsteht. Fährt man in dieser Weise fort, erhält man die Folge der Hexagonalzahlen 1, 6, 15, 28, 45, … . Die zweiunddreißigste Zahl in dieser Folge ist 2016. Man kann zeigen, dass die n-te Hexagonalzahl sich als n(2n – 1) schreiben lässt. Damit ist 2016 = 32·(64 – 1).

Jede Hexagonalzahl ist im Übrigen auch eine Dreieckszahl. Das heißt, man kann 2016 Steine (in der Ebene) so anordnen, dass sie ein ausgefülltes gleichseitiges Dreieck bilden. Die Folge der Dreieckszahlen beginnt mit 1, 3, 6, 10, 15, …. Die zugehörigen Dreiecke haben die Seitenlängen 1, 2, 3, 4, usw. Allgemein gilt: Ist die Seitenlänge n, enthält das Dreieck n(n + 1)/2 Steine. Man rechnet leicht nach, dass das Dreieck mit 2016 Steinen die Seitenlänge n = 63 hat: 2016 = 63×64/2