Juli 2016

Teppiche mit gesiebten Zahlen

Die Themen Primzahlteppiche und Eulersches Primzahlpolynom beschäftigen mich noch immer. Die Idee des Primzahlteppichs stammt von Bartolomé, Rung und Kern¹. In ihrem Buch über Zahlentheorie ist ein Koordinatensystem abgebildet, in dem die Punkte markiert sind, für die der Wert des Terms T(x, y) = x² + y² eine Primzahl ist. Das Muster der Punkte lässt zwar keine große Ordnung erkennen (abgesehen von den trivialen Symmetrien bezüglich der Koordinatenachsen und des Nullpunkts), ist aber nicht zufällig. Variiert man T(x, y), entstehen andere Grafiken.

(1) Hawkins Primes

(2) Lucky Numbers

(3) Primzahlen

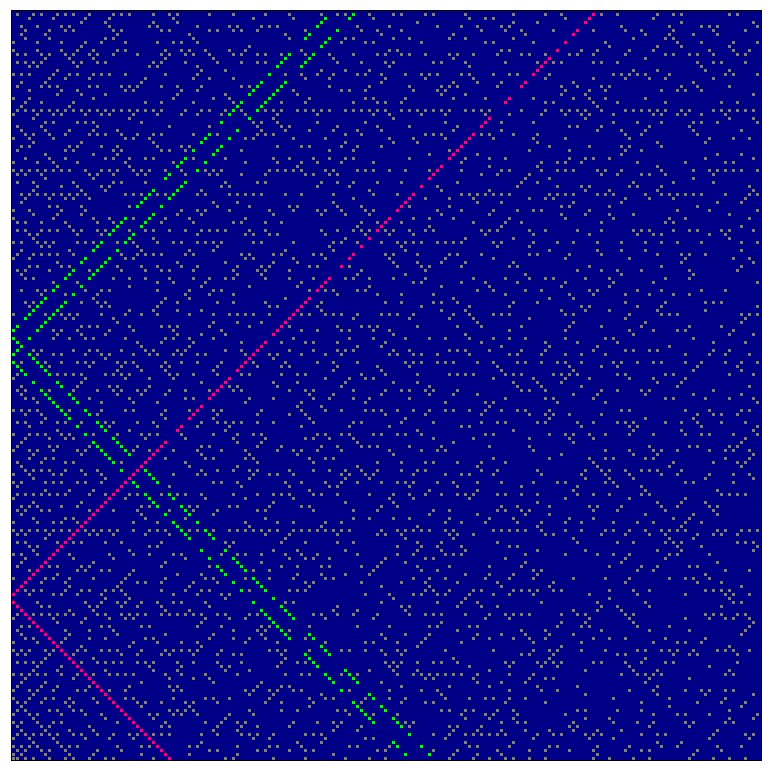
Zahlenteppiche: (1) Random Primes, (2) Lucky Numbers und (3) Primzahlen, siehe Text. Ein Klick auf die Abbildung vergrößert sie.

Meine Idee: Ich erweitere den Begriff des Primzahlteppichs auf den des Zahlenteppichs. Zahlenteppiche sind denmach kartesische Koordinatensysteme, in denen diejenigen Punkte (x, y) markiert werden, für die der Wert eines geeigneten Rechenterms T(x, y) eine Zahl mit einer beliebigen, vorgegebenen Eigenschaft ist. Die Eigenschaft, Primzahl zu sein, wäre somit ein Spezialfall. Wählt man den „richtigen“ Term T(x, y), so dachte ich, müsste es möglich sein, interessante Teppichmuster auch für Zahlenmengen zu erzeugen, die sich durch andere Eigenschaften auszeichnen als prim zu sein.

Ich wähle den Term T(x, y) = x + y². Er liefert einen interessanten Primzahlteppich (dargestellt im Artikel Eulersches Primzahlpolynom). Die Primzahlen werden bekanntlich durch ein Siebverfahren erzeugt, benannt nach seinem Entdecker Eratosthenes. Deshalb liegt es nahe, Zahlen zu testen, die auch durch ein Siebverfahren entstehen. Da gibt es zunächst die „Glücklichen Zahlen“ (engl. Lucky Numbers²). Sie entstehen durch ein Sieb ähnlich dem des Eratosthenes. Es streicht aber die Zahlen im Sieb nicht aufgrund ihres Wertes (wie bei Eratosthenes), sondern aufgrund ihrer Position. Als dritte durch Sieben erzeugte Zahlenmenge soll die Folge der Hawkins Primes³ (oder Random Primes) betrachtet werden. Hawkins’ Sieb ist eine nicht-deterministische, vom Zufall gesteuerte Methode, unter den jeweils verbliebenen Zahlen zu streichen. Hier eine genaue Beschreibung der drei genannten Siebe.

Die Teppiche zum Term T(x, y) = x + y², die den genannten Zahlenmengen Primzahlen, Lucky Numbers und Hawkins Primes entsprechen, sind oben dargestellt. Das Ergebnis ist nicht umwerfend (leider), bestätigt aber unsere intuitive Vorstellung von Ordnung und Chaos in den drei Mengen. Wie erwartet, zeigt der Teppich der Hawkins Primes (Abbildung 1, oben) keinerlei Abweichungen von einer Zufallsverteilung. Die „Glücklichen Zahlen“ (Lucky Numbers) in Abbildung 2 (Mitte) dagegen lassen schon Ketten von Punkten in Richtung der Haupt- und Nebendiagonale erahnen. Im Teppich der Primzahlen (Abbildung 3, unten) schließlich sind diese Ketten zahlreicher und länger geworden – jedenfalls deutlich sichtbar. Zwei dieser Ketten entsprechen den Eulerschen Primzahlen x² ± x + 41, in der Abbildung durch die Farbe Magenta hervorgehoben. Für x < 41 haben sie keine Lücken, bestehen also ausschließlich aus Primzahlen. Für x > 40 ist die überdurchschnittlich große Häufung der Primzahlen auf dem oberen Ast deutlich zu sehen. Die mit grün markierten Primzahlpunkte gehören zu den Termen x² ± x + 101 bzw. x² ± x + 107. Siehe, wie schon erwähnt, den Beitrag Eulersches Primzahlpolynom.

¹ Bartolomé, Andreas, Josef Rung und Hans Kern: Zahlentheorie für Einsteiger (Vieweg 1995), S. 75.
² Hawkins, D., Briggs, W.E.: The Lucky Number Theorem, Mathematics Magazine 31 (1957), 81 – 84, 277 – 280.
³ Hawkins, David: The Random Sieve, Mathematics Magazine 31 (1957), 1 – 3.

Regenbogen – in Natur und Heimversuch

Alles lässt sich an einem einzelnen Wassertropfen erklären. Die Gesetze der Strahlenoptik¹ genügen, um die meisten seiner Eigenschaften zu verstehen: Die Sonnenstrahlen werden beim Eintritt in den Tropfen gebrochen, dann ein- oder mehrmals total reflektiert und beim Austritt wiederum gebrochen. Einmalige Reflexion im Innern des Tropfens führt zum Regenbogen erster Ordnung (Hauptregenbogen), zweimalige Reflexion zum Regenbogen zweiter Ordnung (Nebenregenbogen) usw.

Wem das alles bekannt ist, überspringe die nächsten Zeilen, vielleicht bis zum Stichwort Heimversuch. Der Link dahinter verweist auf Notizen zu einem Modellversuch, bei dem der Wassertropfen durch einen Plexiglaszylinder ersetzt wurde.

Jeder Sonnenstrahl wird aus seiner ursprünglichen Richtung um einen Winkel abgelenkt, der davon abhängt, in welchem Abstand vom Mittelpunkt des Tropfens er einfällt. Verfolgt man den Verlauf vieler Strahlen durch den Tropfen, so stellt man fest, dass es einen kleinsten Ablenkwinkel gibt – und dass in der Umgebung dieses Winkels viele Strahlen zur Ablenkung beitragen. Die Strahlen bilden eine Kaustik (Brennlinie). Das bedeutet, dass hier die Lichtintensität groß ist. Das Auge registriert diese erhöhte Intensität als Regenbogen.

Der kleinste Ablenkwinkel beträgt bei einmaliger Reflexion (Hauptregenbogen) 138°, im Fall zweimaliger Reflexion (Nebenregenbogen) 231°. Am Himmel beobachtet man die Bögen als Kreise um einen imaginären Mittelpunkt, genannt Sonnengegenpunkt (engl. antisolar point). Denkt man sich die Gerade, die vom Beobachter zum Sonnengegenpunkt gerichtet ist, als Bezugsachse, so sieht man den Hauptregenbogen unter dem Winkel 180° – 138° = 42°, den Nebenregenbogen unter dem Winkel 231° – 180° = 51°. Die nachfolgende Skizze zeigt die Strahlen mit kleinstem Ablenkwinkel für Haupt- und Nebenregenbogen (m=1 bzw. m=2). Die Sonne steht dabei tief am Horizont, so dass ihre Strahlen parallel zur Erdoberfläche verlaufen. Die Bezugsachse und der Sonnengegenpunkt liegen in diesem Fall in der Erdoberfläche, und die genannten 42° und 51° sind die Höhenwinkel, unter denen Haupt- bzw. Nebenregenbogen erscheinen.

In den Winkelbereich zwischen 42° und 51° fällt nur wenig Licht. Es stammt von Regenbögen höherer Ordnung, deren Intensität gering ist. Deshalb ist das Gebiet zwischen Haupt-und Nebenregenbogen deutlich dunkler als andere Himmelsbereiche (Alexanders Dunkelzone²). Bei der zweimaligen Brechung des Strahls wird dieser spektral zerlegt, so dass der Ablenkwinkel für die verschiedenen Wellenlängen, die im Licht der Sonne enthalten sind, unterschiedlich ist. Das erklärt die Farben des Regenbogens.

Ersetzt man den Wassertropfen durch einen geeignet geformten Acrylglaskörper, lassen sich einige Eigenschaften des Regenbogens im Heimversuch studieren. Der Versuch war ursprünglich gedacht als Praktikumsexperiment für meine Schüler(innen). Mehr davon hier.

¹ Die strahlenoptische Erklärung des Regenbogens verdanken wir Descartes (1596 – 1650) und Newton (1642 – 1726). Wellenoptische Rechnungen gehen zurück auf Young (1773 – 1829) und Airy (1801 – 1892). Eine Darstellung der Theorie des Regenbogens findet sich beispielsweise in dem Buch von van de Hulst, Light scattering by small Particles, J. Wiley, New York 1957. Von J. D. Jackson (Author des Standardtextes Classical Electrodynamics) stammt eine Kurzfassung der Theorie: From Alexander of Aphrodisias to Young and Airy, Physics Reports 320, (1999), S. 27. Ford und Wheeler behandeln die Regenbogenstreuung als Sonderfall der quantenmechanischen Streuung (in halbklassischer Näherung), Ann. Physics 7, S. 250 (1959). Die exakte Theorie des Regenbogens behandelt die Streuung des Sonnenlichts auf der Grundlage der Maxwell’schen Gleichungen. Numerische Rechnungen dazu wurden z. B. von Nussenzweig ausgeführt (Khare und Nussenzveig, Phys. Rev. Letters 33, S. 976 (1974)). Von Nussenzveig stammt auch eine populärwissenschaftliche Darstellung der Physik des Regenbogens, Scientific American, April 1977, S. 116.

² Benannt nach Alexander von Aphrodisias, Kommentator des Aristoteles, Lehrer am Lyzeum in Athen, ca. 200 n. Chr.