Kategorie: Physik als Hobby

Alles lässt sich an einem einzelnen Wassertropfen erklären. Die Gesetze der Strahlenoptik¹ genügen, um die meisten seiner Eigenschaften zu verstehen: Die Sonnenstrahlen werden beim Eintritt in den Tropfen gebrochen, dann ein- oder mehrmals total reflektiert und beim Austritt wiederum gebrochen. Einmalige Reflexion im Innern des Tropfens führt zum Regenbogen erster Ordnung (Hauptregenbogen), zweimalige Reflexion zum Regenbogen zweiter Ordnung (Nebenregenbogen) usw.

Wem das alles bekannt ist, überspringe die nächsten Zeilen, vielleicht bis zum Stichwort Heimversuch. Der Link dahinter verweist auf Notizen zu einem Modellversuch, bei dem der Wassertropfen durch einen Plexiglaszylinder ersetzt wurde.

Jeder Sonnenstrahl wird aus seiner ursprünglichen Richtung um einen Winkel abgelenkt, der davon abhängt, in welchem Abstand vom Mittelpunkt des Tropfens er einfällt. Verfolgt man den Verlauf vieler Strahlen durch den Tropfen, so stellt man fest, dass es einen kleinsten Ablenkwinkel gibt –  und dass in der Umgebung dieses Winkels viele Strahlen zur Ablenkung beitragen. Die Strahlen bilden eine Kaustik (Brennlinie). Das bedeutet, dass hier die Lichtintensität groß ist. Das Auge registriert diese erhöhte Intensität als Regenbogen.

Der kleinste Ablenkwinkel beträgt bei einmaliger Reflexion (Hauptregenbogen) 138°, im Fall zweimaliger Reflexion (Nebenregenbogen) 231°.  Am Himmel beobachtet man die Bögen als Kreise um einen imaginären Mittelpunkt, genannt Sonnengegenpunkt (engl. antisolar point). Denkt man sich die Gerade, die vom Beobachter zum Sonnengegenpunkt gerichtet ist, als Bezugsachse, so sieht man den Hauptregenbogen unter dem Winkel 180° – 138° = 42°, den Nebenregenbogen unter dem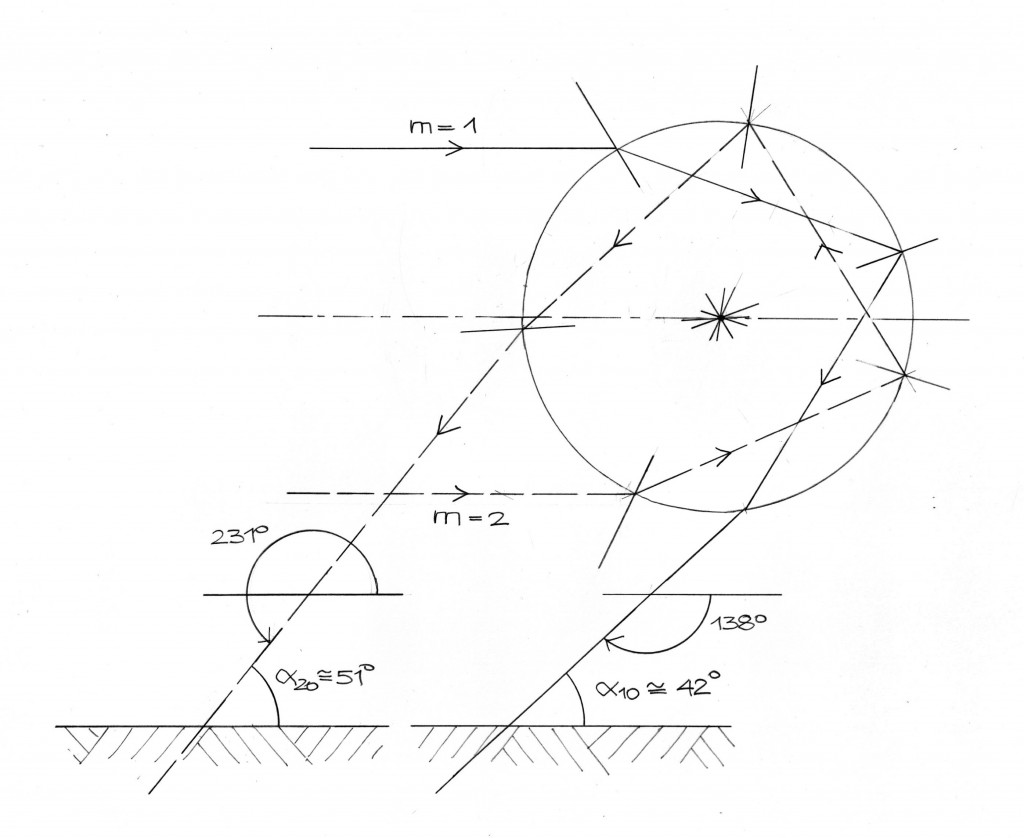 Winkel 231° – 180° = 51°. Die nachfolgende Skizze zeigt die Strahlen mit kleinstem Ablenkwinkel für Haupt- und Nebenregenbogen (m=1 bzw. m=2). Die Sonne steht dabei tief am Horizont, so dass ihre Strahlen parallel zur Erdoberfläche verlaufen. Die Bezugsachse und der Sonnengegenpunkt liegen in diesem Fall in der Erdoberfläche, und die genannten 42° und 51° sind die Höhenwinkel, unter denen  Haupt- bzw. Nebenregenbogen erscheinen.

In den Winkelbereich zwischen 42° und 51° fällt nur wenig Licht. Es stammt von Regenbögen höherer Ordnung, deren Intensität gering ist. Deshalb ist das Gebiet zwischen Haupt-und Nebenregenbogen deutlich dunkler als andere Himmelsbereiche (Alexanders Dunkelzone²). Bei der zweimaligen Brechung des Strahls wird dieser spektral zerlegt, so dass der Ablenkwinkel  für die verschiedenen Wellenlängen, die im Licht der Sonne enthalten sind, unterschiedlich ist. Das erklärt die Farben des Regenbogens.

Ersetzt man den Wassertropfen durch einen geeignet geformten Acrylglaskörper, lassen sich einige Eigenschaften des Regenbogens im Heimversuch studieren. Der Versuch war ursprünglich gedacht als Praktikumsexperiment für meine Schüler(innen). Mehr davon hier.

¹  Die strahlenoptische Erklärung des Regenbogens verdanken wir Descartes (1596 – 1650) und Newton  (1642 – 1726). Wellenoptische Rechnungen gehen zurück auf Young (1773 – 1829) und Airy (1801 – 1892). Eine Darstellung der Theorie des Regenbogens findet sich beispielsweise in dem Buch von van de Hulst, Light scattering by small Particles,  J. Wiley, New York 1957. Von J. D.  Jackson (Author des Standardtextes Classical Electrodynamics) stammt eine Kurzfassung der Theorie: From Alexander of Aphrodisias to Young and Airy, Physics Reports 320, (1999), S. 27. Ford und Wheeler  behandeln die Regenbogenstreuung als Sonderfall der quantenmechanischen Streuung (in halbklassischer Näherung),  Ann. Physics 7, S. 250 (1959).  Die exakte Theorie des Regenbogens behandelt die Streuung des Sonnenlichts auf der Grundlage der Maxwell’schen Gleichungen. Numerische Rechnungen dazu wurden z. B. von Nussenzweig  ausgeführt (Khare und Nussenzveig, Phys. Rev. Letters 33, S. 976 (1974)). Von Nussenzveig stammt auch eine populärwissenschaftliche Darstellung der Physik des Regenbogens, Scientific American, April 1977, S. 116.

²  Benannt nach Alexander von Aphrodisias, Kommentator des Aristoteles, Lehrer am Lyzeum in Athen, ca. 200 n. Chr.

Ein Brett mit Eisennägeln, kein Uecker: Das Foto zeigt den Aufbau eines Physikexperiments – die Streuung von Hochfrequenzwellen an einem Kristall-Modell. Modell deswegen, weil der Versuch in der professionellen Physik an einem (optischen) Kristall mit Lichtwellen ausgeführt wird. Dort ist er mit dem Namen Bragg-Reflexion verknüpft. In der Schule benutzte ich die Modellversion mehrmals als Thema für Abiturklausuren (damals, als es noch kein Zentralabitur gab). Die Experimente dazu standen unter Zeitdruck: meist kam man erst in den Winterferien dazu, über Abiturthemen nachzudenken und die dazu passenden Experimente auszutüfteln. Am Ende der Ferien mussten die die Experimente funktionieren und die Aufgabenvorschläge fertig sein. An das hektische Experimentieren im ungeheizten Schulgebäude (in den Ferien) erinnere ich mich noch. Die Messdaten schlummerten seitdem in meinen Protokollbüchern. Ich habe sie jetzt noch ein Mal hervorgeholt und in Ruhe ausgewertet. Hier sind die Resultate.

Die Pfeife einer Orgel bringt einen Ton hervor, weil die Luftmoleküle sich in ihrem Innern hin- und herbewegen und dabei örtlich Verdichtungen und Verdünnungen der Luft erzeugen. Diese dringen nach Außen und gelangen als Schallwellen an unser Ohr. Eine Orgelpfeife ist im Prinzip ein langgestrecktes Rohr. Wenn man berechnen will, welchen Ton das Rohr hervorbring, macht man üblicherweise die Annahme, dass an seinen Enden der Dichte- oder Druckunterschied zur Außenluft Null ist. Die Schwingung hat, wie man sagt, an den Enden des Rohrs einen Knoten.  Aber eben diese Annahme ist physikalisch fragwürdig. Sie bedeutet, dass die Luftmoleküle „draußen“ von der Schwingung im Innern der Pfeife in keiner Weise „mitgerissen“ werden. Das heißt, die Pfeife würde keinerlei Schall abstrahlen.

Zu erklären, wie eine Pfeife Schall abstrahlt, ist kein triviales Problem. Eine aufwändige Rechnung ergibt, dass die Luftmoleküle, vereinfacht ausgedrückt, über die Enden des Rohrs hinausschwingen und so der Schall nach draußen getragen wird. Das heißt, die Pfeife ist effektiv länger als mit dem Maßband gemessen. Levine und Schwinger¹ berechneten, dass die Verlängerung je Ende etwa das 0,6-fache des Rohrradius beträgt. Diese Zahl ist die berühmte Endkorrektur.  Man muss sie berücksichtigen, wenn man aus der Länge der Pfeife die Höhe des Tons berechnen will, der abgestrahlt wird. Die Endkorrektur lässt sich mit einfachen Mitteln experimentell bestimmen. Details hier.

Foto: Orgel der Kirche Divi Blasii in Mühlhausen/Thüringen, gebaut nach einem Entwurf von Johann Sebastian Bach

¹ Levine, H. und J. Schwinger, Phys. Rev. 73, 383 (1948)

Jeder Hochfrequenz-Profi (damit meine ich insbesondere meine Amateurfunkfreunde) kennt das Strahlungsdiagramm eines λ/2-Dipols. Aber gemessen haben es die wenigsten. Das nebenstehende Diagramm zeigt das Ergebnis einer eigenen (unvollständigen) Messung, ich entdeckte es vor kurzem in meinen Unterrichtsaufzeichnungen aus grauer Vorzeit.

Offenbar reichte die Zeit nicht aus, das vollständige Diagramm zu messen. Hier könnte also experimentell noch nachgebessert werden. Bis es dazu kommt, dachte ich, ist eine Beschäftigung mit der Theorie nicht unvernünftig. Erste Möglichkeit, mich kundig zu machen, waren meine Notizen zur Vorlesung „Elektrodynamik“ (aus dunkelgrauer Vorzeit). Die waren noch erstaunlich gut lesbar¹, ergaben aber Nachholbedarf in Sachen Vektorpotential und Lorenz-Eichung. Die Bücher von Griffiths und Jackson² halfen da weiter. Beim Studium dieser Werke entdeckte ich, dass man sogar den Gewinn des λ/2-Dipols gegenüber dem isotropen Strahler, also die rätselhaften 2,15 dBi, herleiten kann. Aber wie so oft, hieß es mehrfach: „Wie man leicht nachrechnet, ergibt sich ….“. Diese Lücken habe ich versucht, aufzufüllen. Hier das Ergebnis meiner zwei „Ausarbeitungen“ –  eine zum (idealen) Hertzschen Dipol und eine andere zum λ/2-Dipol.

¹ Das spricht für meine saubere Handschrift und Prof. Scherzers glasklaren Tafelanschrieb. Professor Scherzer las damals die Theoretische Physik an der TH Darmstadt. Der Tafelanschrieb startete am Anfang der Vorlesung in der linken oberen Ecke der Tafel, schlängelte sich ohne aufwändige Gliederung unter Ausnutzung der gesamten Tafelbreite zeilenweise nach unten und erreichte zeitgleich mit dem Ende der Stunde die rechte untere Ecke. Die jederzeit verfügbare Darstellung des Unterrichtsstoffs erlaubte es, beim Mitschreiben auf Schönschrift zu achten.

²  David J. Griffiths, Elektrodynamik – Eine Einführung, 3. Auflage, Pearson Studium, München 2011, und  John D. Jackson, Classical Electrodynamics, J. Wiley, New York 1962

Read more

Physik muss ich nicht mehr unterrichten. Meine Unterrichtsunterlagen sind entsorgt, nur einen Teil habe ich aus sentimentalen Gründen aufbewahrt. Beim Stöbern in den vergilbten Blättern fielen mir zwei Farbfotos in die Hände – von mir aufgenommene Linienspektren, die meine Schüler(innen) damals auswerten mussten (Klausuraufgabe). Die Fotos sind keine Meisterwerke, aber sie einfach wegzuwerfen wäre schade. Deshalb eine kurze Nachlese.

Das Foto zeigt die Spektren des Wasserstoffs (unten) und des Heliums (oben). Die weiße Linie links ist das Bild der Lichtquelle in Vorwärtsrichtung. Das Helium-Spektrum sollte zur Eichung herangezogen werden. Im Spektrum des Wasserstoffs sind die Balmer-Linien H_α, H_β und H_γ sichtbar.

Glas lässt Licht hindurchtreten (das ist die Transmission) und/oder wirft es zurück (dann spricht man von Reflexion*). Die Physik dazu interessiert uns hier ausnahmsweise nicht, wir betrachten Beispiele aus der Architektur, bei denen Glas und Licht im Spiel sind. Die Fotos sind nicht das Ergebnis gezielter Suche, sie entstanden eher beiläufig.

Nebenstehendes Bild: In der Glasfassade des Fontainebleau Resort Hotels (einer Bauruine) in Las Vegas  spiegelt sich das Nachbar-Hochhaus.

 * Pardon, hier spricht wieder einmal der Lehrer. Wer auch noch wissen will, woher die beiden Wörter Transmission und Reflexion stammen, schaut im Wörterbuch nach:  transmittere (lat.): hinüberschicken, hinüberbringen;  reflectere (lat.): rückwärts biegen, zurückdrehen, zurückwenden

Wir kleben Streifen einer Klebefolie (Tesafilm) parallel versetzt auf das Glas eines Dia-Rähmchens. Dadurch entstehen Bereiche unterschiedlicher Dicke des Folienmaterials. Das Glas halten wir zwischen zwei (mehr oder weniger) gekreuzte Polarisationsfilter – und sehen die Folienstreifen in verschiedenen Farben aufleuchten (Foto). Der Effekt ist bekannt, und wir wissen auch, wie er zustande kommt: Die erste Polarisationsfolie erzeugt linear polarisiertes Licht. Dieses wird aufgrund der doppelbrechenden Eigenschaft der Klebefolie zu elliptisch polarisiertem Licht. Die Orientierung der Ellipsenachsen ist von der Dicke des Materials und der Wellenlänge des Lichtes abhängig. Die zweite Polarisationsfolie wirkt als Analysator, der je nach Ausrichtung Licht einer Wellenlänge hindurch lässt, Licht anderer Wellenlänge unterdrückt.

Hier ist also Doppelbrechung im Spiel – die Theorie dazu ist interessant, aber mit etwas Rechnen verbunden.

Selbst an einem kalten Wintertag wärmt uns die Sonne durch ihre Strahlung – sofern sie am Himmel steht. Der Physiker möchte nicht nur wissen, ob die Sonne strahlt, sondern auch wie stark sie das tut. Die Größe, in der man das ausdrückt, heißt Bestrahlungsstärke. Sie gibt an, mit welcher Leistung pro Quadratmeter (Kilowatt/m²) die Strahlung die Erde trifft. Die Zahl selbst heißt Solarkonstante.

Das Foto zeigt eine Anordnung, mit der man diese Größe messen kann. Ausführliche Beschreibung des Experiments.

Zur Lehrerausbildung gehört die Praxis: Als angehender Physiklehrer musste ich, wie üblich, Experimente vorführen. An eines dieser Demonstrationsexperimente erinnere ich mich noch sehr gut.

Gezeigt werden sollte die Wirkung der Gravitationskraft, also der Kraft, mit der sich zwei Massen gegenseitig anziehen. Dazu benutzt man die von Coulomb erfundene und später von  Cavendish benutzte Drehwaage – ein Gerät, das wegen seiner großen Schwingungsdauer nicht ganz einfach zu handhaben ist. Links eine Skizze dieses Geräts.

Ich hatte die Drehwaage am Vortag zwei Stunden lang auspendeln lassen, damit sie in der Unterrichtsstunde am Tag darauf eine definierte Ruhelage hatte. Dann geschah die Katastrophe:

Read more