Kategorie: Physik als Hobby

Keine hebräischen Schriftzeichen und auch keine mystischen Kultsymbole, sondern Salzkörner auf einer schwarzen Stahlplatte – das zeigt die nebenstehende Abbildung. Es handelt sich um Chladnische Klangfiguren, benannt nach ihrem Entdecker Ernst Florens Chladni (1756 – 1827).

Man erzeugt diese Figuren, indem man eine  waagerecht liegende, dünne Metallplatte mit Sand (in unserem Fall Salz) bestreut und in Schwingungen versetzt. Das erreicht man beispielsweise, indem man die Platte von unten mit einem Lautsprecher beschallt, der einen reinen Sinuston abstrahlt.

Read more

Resonanzkurven haben einen gewissen ästhetischen Reiz. Ein Beispiel zeigt die Abbildung. Sie ist das Ergebnis einer Messung an einem Federpendel.

Wir hängen ein Gewichtsstück an eine Schraubenfeder und bewegen das obere Ende der Feder mit der Hand auf und ab. Dabei gerät das Gewichtsstück in Schwingungen. Treffen wir den richtigen Takt beim Auf- und Ab-Bewegen der Feder, schwingt das Gewichtsstück sehr weit aus – wir regen die Schwingung in Resonanz an. Die Resonanzkurve gibt an, wie weit das Federpendel bei verschiedenen Taktfrequenzen ausschlägt. In unserem Fall ist die Schwingungsweite („Amplitude“)  am größten, wenn man die Feder etwa einmal pro Sekunde  auf- und ab bewegt. Das heißt, die Resonanzfrequenz ist 1 Hertz (Hz). Mehr über die Resonanzkurve eines Federpendels.

Goldener Schnitt und Physik haben nicht viel gemeinsam, sollte man meinen. Stimmt nicht – eine Aufgabe aus der Elektrizitätslehre zeigt das. Das nachfolgende Beispiel stammt auch aus der Physik und ist in Fachkreisen sicher bekannt. Mir fiel jetzt ein, dass ich es vor Jahren einmal nachgerechnet habe. Danach vergaß ich es – das hat es nicht verdient. Also eine kleine Neuauflage des Problems. Es geht um ein L-förmiges Stück Karton.

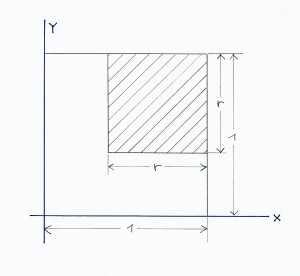
Abb. 1

Wir starten mit einem quadratischen Stück Karton. Aus diesem Quadrat soll ein kleineres Quadrat an der rechten oberen Ecke herausgeschnitten werden, dessen Seiten parallel zu denen des größeren Quadrats sind. Übrig bleibt ein L-förmiges Kartongebilde mit gleich langen Schenkeln. Dieses soll am Schnittpunkt der Schenkel-Innenkanten so aufgehängt werden, dass seine Schenkel in der Waagerechten sind. Frage: Wie groß muss die Kantenlänge des herausgeschnittenen Quadrats sein, bezogen auf die Kantenlänge des ursprünglichen Quadrats, damit dies der Fall ist?

Man sieht sofort ein, dass der Aufhängepunkt der Schwerpunkt der L-förmigen Restfläche sein muss. Wir müssen daher die Lage dieses Schwerpunkts berechnen, und zwar in Abhängigkeit von der Kantenlänge des herausgeschnittenen Quadrats.

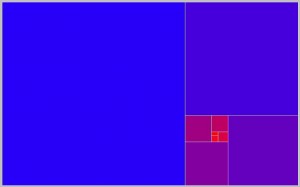
Um die Rechnung zu vereinfachen, setzen wir die Kantenlänge des ursprünglichen Quadrats gleich 1 (Eins). Die Kantenlänge des herausgeschnittenen Quadrats sei r genannt. Es ist nun sinnvoll, ein (rechtwinkliges) Koordinatensystem zugrunde zu legen, dessen Ursprung mit der linken unteren Ecke des ursprünglichen Quadrats zusammen fällt, und dessen Achsen sich in Richtung der unteren Kante (x-Achse) bzw. linken Kante (y-Achse) dieses Quadrats erstrecken (Abb. 1).

Abb. 2 Das ausbalancierte L (rot)

Die Rechnung ergibt, dass r der Gleichung   r³   –  2r  +  1  =   0 genügen muss. Die positiven Lösungen dieser Gleichung sind r = 1 oder r = 0,61803398… . Das heißt, der Schnittpunkt der Schenkel-Innenkanten des „L“  liegt entweder bei ( x, y )   =  (1, 1)  oder bei ( x, y )   =   (0,618…, 0,618…). Die erste Lösung  (1, 1)   entspricht einem „L“ mit Flächeninhalt Null, sie ist physikalisch nicht zu realisieren. Bei der zweiten hingegen liegt der Schwerpunkt innerhalb der Fläche des ursprünglichen Quadrats, und zwar im „Goldenen Schnitt“ der Quadratseiten¹. Abb. 2 zeigt ein solches ausbalanciertes L.

¹ Alles über den Goldenen Schnitt steht z. B. bei A. Beutelspacher und B. Petri: Der Goldene Schnitt, BI-Verlag, Mannheim 1989

Drei Verstärkerschaltungen auf Experimentierplatine

Unter uns Funkamateuren vom (DARC-) Ortsverband Mönchengladbach kam der Wunsch auf, einfache elektronische Schaltungen einmal selbst zu bauen – und, soweit möglich, auch zu verstehen. Zugegeben, keine originelle Idee, aber eine, die offenbar voll im Trend liegt: Die Zeit der Maker ist angebrochen, lesen wir überall.

Unser erstes Projekt, zum „Warmlaufen“: eine einfache NF-Verstärkerstufe. Damit das Löten nicht gleich zu Anfang ein Hindernis war, wurde sie auf einer Experimentierplatine aufgebaut. Das machte auch keine Probleme. Das Foto zeigt die Platine mit drei verschiedenen Verstärkerstufen – links mit einem bipolaren npn-Transistor (BC 547C), in der Mitte mit einem MOSFET (BS 170) und rechts mit einem JFET (BF 245C).

Die Schaltungen funktionierten. Aber dann wollten wir wissen, wie man die Werte der Widerstände und Kondensatoren berechnet, die dort eingesetzt wurden – beispielsweise in der Schaltung mit dem npn-Transistor. Dazu ein Rechenbeispiel (Die Betonung liegt auf Beispiel: Beim praktischen Aufbau stellte sich heraus, dass die entsprechende Schaltung noch verbessert werden könnte).

Im Artikel Foucault-Pendel fehlten Details zum Versuchsaufbau und zum eigentlichen Experiment. Die sollten nachgeliefert werden. Daraus wird leider nichts, die Unterlagen sind verschollen.  Deshalb habe ich das Pendel noch einmal aufgebaut – in der gleichen Anordnung wie vor einigen Jahren. Die elektronische Steuerung funktionierte zwar nach einigen Eingriffen, aber das Pendel dachte nicht daran, seine Schwingungsebene zu verändern. Der Grund dafür, vermutete ich, war das Stahlseil, das ich als Pendelaufhängung benutzte (zu starr, zu sehr verdrillt, oder …?). Mit einem Kunststoffseil drehte sich die Schwingungsebene wieder – aber dafür verlängerte sich das Seil während des Experiments. Nach etwa drei Stunden streifte der Magnet an der Unterseite der Pendelkugel den Eisenkern der Antriebsspule. Damit fand die Schwingung ein jähes Ende. Immerhin ergab eine erste Messung (über ein Zeitintervall von ca. einer Stunde) den richtigen Wert für die Präzessionsrate (Abb. unten). Sie betrug 11,8 ±  0,4 Grad/Stunde – der theoretische Wert ist 11,7 Grad/Stunde. Also ein bescheidener Erfolg. Die  Abbildung links oben zeigt das Pendel mit einem darunter angebrachten Winkelmesser. Mit etwas Geduld und einer ruhigen Hand gelingt es, die optische Achse der Kamera in die Schwingungsebene des Pendels zu bringen. Dann markiert der Pendelfaden auf dem Foto den momentanen Winkel der Schwingungsebene.

Zum Schluss zwei Bemerkungen zur Theorie: (1) Die Herleitung der Formel für den Drehwinkel der Schwingungsebene eines Foucault-Pendels ist eine kleine Übung in Newtonscher Mechanik für rotierende Systeme. (2) Leider dreht sich die Schwingungsebene auch dann, wenn das Pendel nicht geradlinig schwingt, sondern eine elliptische Bahn durchläuft (Deshalb muss diese Bewegung gedämpft werden, zum Beispiel durch den Charron-Ring). Die Winkelgeschwindigkeit dieser „elliptischen“ Präzession ist proportional zum Flächeninhalt der Bahnellipse. Sie auszurechnen ist eine etwas umfangreichere mathematische Trainingseinheit.

Band III des Berkeley-Kurses Physik („Waves“) ist eine Fundgrube für Anregungen zu Hobby-Experimenten – mit interessanten physikalischen Fragestellungen. Im Buch heißen sie „home experiments“. Beispielsweise modelliert Frank S. Crawford, der Autor des Buchs, erzwungene Schwingungen eines Plasmas mit denen einer Reihe gekoppelter Pendel. Die Pendel sind Fadenpendel gleicher Pendelmasse M und gleicher Länge L. Sie bilden eine lineare Kette mit gegenseitigem Abstand a und werden durch Federn mit der Federkonstante K gekoppelt (Abb. unten).

Die Kreisfrequenz der freien Schwingung jedes Pendels entspricht der Plasmafrequenz. Sie ist gegeben durch ω**₂ = g/L (Dabei ist g = 9,81 m/s**² die Fallbeschleunigung). Mit dieser Frequenz schwingen alle Pendel (und zwar mit gleicher Phase), wenn die Koppelfedern weder gestreckt noch gestaucht werden. 

Besonders eindrucksvoll sind Experimente mit einer Pendelkette, bei der sich die Pendellänge L an einer Stelle sprunghaft ändert (oder bei der die Kette am Ende befestigt ist). Zur Anregung versetzt man das Pendel am Anfang der Kette in eine harmonische Bewegung (in Längsrichtung). Dann sieht man, dass bei gewissen Anregungsfrequenzen einige Pendel mit großer Amplitude schwingen. Solche Resonanzen habe ich vor vielen Jahren untersucht. Ich finde die Ergebnisse immer noch höchst interessant. Mehr

Elektronenablenkröhre

Die Physiksammlung einer Schule ist voller High-Tech-Geräte. Viele Geräte werden oft nur in wenigen Routine-Versuchen eingesetzt. Sie lassen sich aber auch etwas außerhalb der gängigen Praxis „beschäftigen“. Das führt manchmal zu interessanten Experimenten. Eine Elektronen-Ablenkröhre zum Beispiel macht die Bahnen bewegter Elektronen im Vakuum sichtbar. Setzt man die Elektronen einem Magnetfeld aus, sind das Kreise in einer Ebene senkrecht zu den magnetischen Feldlinien. Das Magnetfeld wird üblicherweise durch ein Helmholtzspulenpaar erzeugt. Aber auch ohne Helmholtzspulen kreisen die Elektronen in der Röhre, denn sie werden im Magnetfeld der Erde abgelenkt. Das kann man trotz der geringen Feldstärke des Erdfeldes sichtbar machen – sogar die Stärke des Feldes lässt sich messen. Die Abbildung zeigt eine Elektronenablenkröhre bei der Messung des Erdfeldes. Mehr zu diesem Versuch.

Ein „goldenes“ Rechteck

Impedanz ist ein anderes Wort für Wechselstromwiderstand. Es geht also um Elektrotechnik. Um einen Stromkreis, dessen Impedanz von der Frequenz der Stromquelle abhängt. Die Einzelheiten später.

Zunächst zum Goldenen Schnitt: Wir zeichnen ein Rechteck, dessen Länge sich zur Breite verhält wie (√5 + 1)/2 zu 1,  oder näherungsweise wie 1,618 zu 1. Spaltet man das größte Quadrat ab, das hineinpasst, bleibt ein Rechteck übrig mit demselben Seitenverhältnis. Aus diesem entfernt man wiederum das größte einbeschriebene Quadrat, und wiederum bleibt ein Rechteck übrig, dessen Seitenlängen sich wie (√5 + 1)/2 zu 1 verhalten. Das Spiel lässt sich ad infinitum fortsetzen – aber nur dann, wenn man wie oben mit dem genannten Seitenverhältnis beginnt. In der Abbildung sind die ersten Schritte erkennbar. Die Zahlen (√5 + 1)/2 = 1,618339…  und (√5 – 1)/2 = 0,618339… , die hier eine Rolle spielen, sind die Teilungsverhältnisse des Goldenen Schnitts. In der Kunst soll er besonders angenehme Proportionen erzeugen. Dass er auch in anderen Bereichen „mitmischt“, ist bekannt.

Ein Beispiel aus der Elektrotechnik ist der nachfolgende Wechselstromkreis. Seine Impedanz

Stromlaufplan unserer Schaltung

(sein Wechselstromwiderstand) ist Null für zwei Kreisfrequenzen, die durch die Resonanzfrequenz 1/√LC der Einzelkreise im Verhältnis des Goldenen Schnitts geteilt wird. Mehr

Abbildung: Bahnen von Erde und Jupiter und Bestimmung der Entfernung Jupiter-Erde. O: Jupiter in Opposition zur Sonne (nachts), K: Jupiter in Konjunktion zur Sonne (am Tage). Entfernungen in astronomischer Einheit AE (1 AE = 149,6 Millionen km)

Ein geniales „Experiment“, am Schreibtisch nachempfunden: Ole Rømers Bestimmung der Lichtgeschwindigkeit.

Zuvor einige Erläuterungen zu Messmethode: Schon Galilei richtete nachts sein Fernrohr auf den Planeten Jupiter und stellte fest, das dieser von Monden umkreist wird. Damit waren Jupiter und seine Monde das erste System, an dem man durch Beobachtung von „Außen“ die Bewegung von Satelliten studieren konnte. Ole Rømer untersuchte das Kreisen der Jupitermonde genauer. Und prompt entdeckte er, dass einer der Monde, nämlich Io, es mit den Gesetzen der Physik offenbar nicht so genau hielt: Seine beobachtete Umlaufzeit wurde größer, je weiter sich die Erde vom Jupiter und damit von ihm, dem Mond Io, entfernte. Wie kommt es dazu?

Die (synodische) Umlaufzeit des Jupitermondes Io beträgt T_Io = 1,76986 Tage (d). Dies ist die Zeitspanne, die beispielsweise verstreicht zwischen zwei aufeinanderfolgenden Austritten dieses Mondes aus dem Kernschatten des Jupiters (Verfinsterungsende). Rømer bestimmte die Zeitpunkte der Verfinsterungsenden über längere Zeit hinweg. Um seine Vorgehensweise nachzuvollziehen, nehmen wir an, dass Jupiter am Anfang seiner Beobachtungsreihe in Opposition zur Sonne stand. Die Erde befindet sich dabei im Punkt O der Abbildung, so dass die Entfernung zwischen Jupiter und Erde minimal war. In der Folgezeit nahm der Abstand zwischen Erde und Jupiter fortlaufend zu, da sich die Erde in Richtung Konjunktionsstellung (Punkt K in der Abbildung) bewegte, während Jupiter wegen seiner 12-jährigen Umlaufzeit praktisch auf der Stelle trat. Rømer stellte fest, dass die Verfinsterungsenden im Laufe der Zeit immer später eintrafen als vorherberechnet. Das heißt, das Verfinsterungsende nach beispielsweise 90 Io-Umläufen trat nicht genau 90 ×1,76986 Tage später ein als das erste von ihm beobachtete Verfinsterungsende, sondern hinkte einige Minuten hinterher. Er zog daraus den richtigen Schluss, dass diese Verzögerung der Zeitdauer entspricht, die das Licht benötigt, um die Entfernungsdifferenz zwischen den Positionen der Erde am Anfang und Ende der Beobachtungsreihe zurückzulegen.

Verzögerung und Entfernungsdifferenz lassen sich aus Ephemeridentabellen bzw. astronomischen Tafelwerken ermitteln. Die Rechnung ergibt beispielsweise, dass für eine Entfernungsdifferenz von 150,1 Millionen Kilometern die Verzögerung 9,28 Minuten = 557,1 Sekunden beträgt. Daraus folgt für die Lichtgeschwindigkeit ein Wert von c = 269500 km/s. Nimmt man an, dass die Verzögerung auf etwa ± 2 Minuten genau bestimmt werden kann, ergibt sich für die Lichtgeschwindigkeit einschließlich Fehler c = (269500 ± 58100) km/s. Dieser Wert ist innerhalb der Fehlergrenzen mit dem Literaturwert c = 299792,458 km/s verträglich. 

Galilei ließ Kugeln aus verschiedenem Material zur Erde fallen (der Überlieferung nach vom schiefen Turm zu Pisa) – und stellte fest, dass alle zur gleichen Zeit auf den Boden aufschlugen. Im Physikunterricht kam die Frage auf, wie genau man das mit einfachen Mitteln nachprüfen könne – und in wie weit man dabei den Literaturwert der Fallbeschleunigung (g = 9,81 m/s²) messen würde.

Abb. 1 Ultraschall-Entfernungsmesser im Treppenhaus der Schule

Unsere Körper waren Kugeln mit (fast) gleichem Durchmesser, und zwar ein Tischtennisball (Masse 0,003 kg, Durchmesser 3,8 cm), eine Stahlkugel (Masse 0,229 kg, Durchmesser 3,8 cm) und eine Holzkugel (Masse 0,035 kg, Durchmesser 4,4 cm). Sie durchfielen eine Strecke von ca. 2 m. Ihre Bewegung wurde mit einem Ultraschall-Entfernungsmesser (CBR) gemessen. Dieses Gerät befand sich senkrecht über dem Punkt, an dem die Kugel losgelassen wurde. Das Foto Abb. 1 zeigt den Versuchsaufbau im Treppenhaus der Schule. Der Entfernungsmesser befindet sich am linken Ende der Holzstange. Rechts erkennt man den Datenlogger (TI83).  Zur Zeit der Fotoaufnahme werden gerade die Daten des vorhergehenden Versuchs ausgelesen. Deshalb ist die Verbindung zwischen Entfernungsmesser und Datenlogger unterbrochen. Während einer Messung steckt das Kabel des Ultraschallgeräts natürlich in der Eingangsbuchse des Datenloggers.

Read more