Selbst an einem kalten Wintertag wärmt uns die Sonne durch ihre Strahlung – sofern sie am Himmel steht. Der Physiker möchte nicht nur wissen, ob die Sonne strahlt, sondern auch wie stark sie das tut. Die Größe, in der man das ausdrückt, heißt Bestrahlungsstärke. Sie gibt an, mit welcher Leistung pro Quadratmeter (Kilowatt/m²) die Strahlung die Erde trifft. Die Zahl selbst heißt Solarkonstante.

Das Foto zeigt eine Anordnung, mit der man diese Größe messen kann. Ausführliche Beschreibung des Experiments.

Zur Lehrerausbildung gehört die Praxis: Als angehender Physiklehrer musste ich, wie üblich, Experimente vorführen. An eines dieser Demonstrationsexperimente erinnere ich mich noch sehr gut.

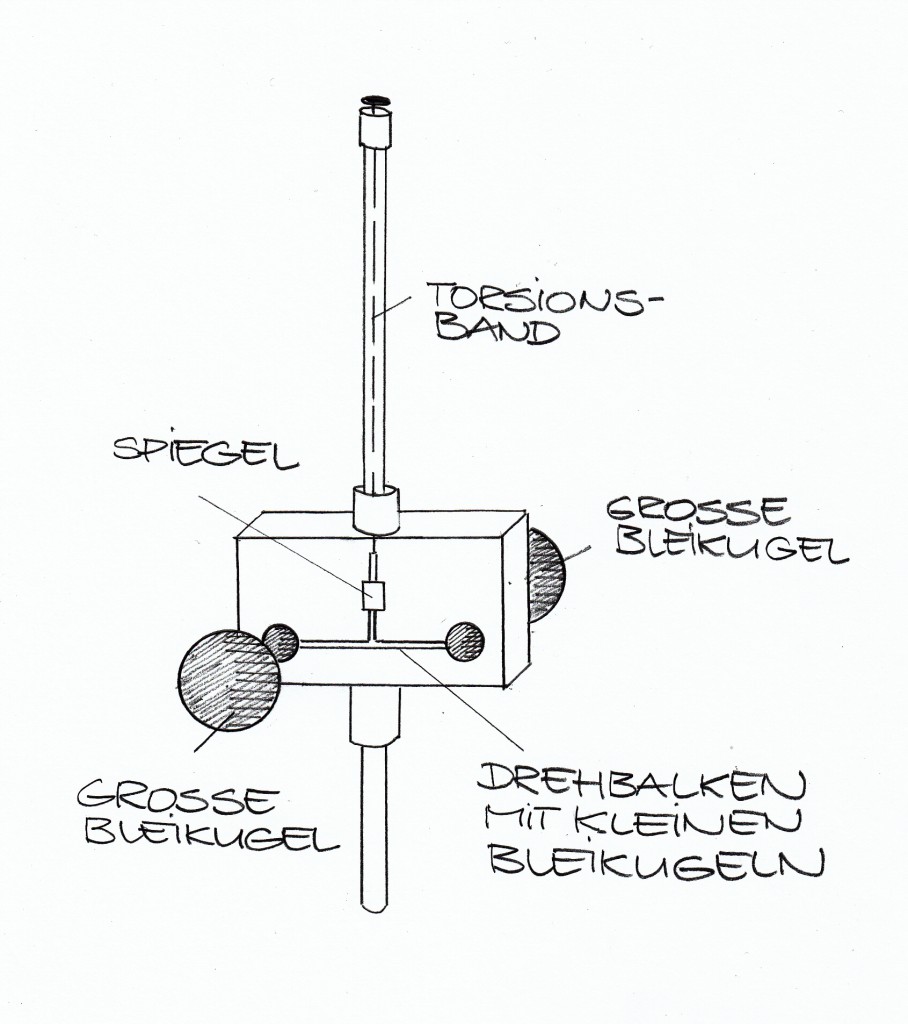
Gezeigt werden sollte die Wirkung der Gravitationskraft, also der Kraft, mit der sich zwei Massen gegenseitig anziehen. Dazu benutzt man die von Coulomb erfundene und später von  Cavendish benutzte Drehwaage – ein Gerät, das wegen seiner großen Schwingungsdauer nicht ganz einfach zu handhaben ist. Links eine Skizze dieses Geräts.

Ich hatte die Drehwaage am Vortag zwei Stunden lang auspendeln lassen, damit sie in der Unterrichtsstunde am Tag darauf eine definierte Ruhelage hatte. Dann geschah die Katastrophe:

Read more

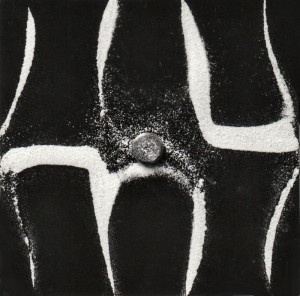
Keine hebräischen Schriftzeichen und auch keine mystischen Kultsymbole, sondern Salzkörner auf einer schwarzen Stahlplatte – das zeigt die nebenstehende Abbildung. Es handelt sich um Chladnische Klangfiguren, benannt nach ihrem Entdecker Ernst Florens Chladni (1756 – 1827).

Man erzeugt diese Figuren, indem man eine  waagerecht liegende, dünne Metallplatte mit Sand (in unserem Fall Salz) bestreut und in Schwingungen versetzt. Das erreicht man beispielsweise, indem man die Platte von unten mit einem Lautsprecher beschallt, der einen reinen Sinuston abstrahlt.

Read more

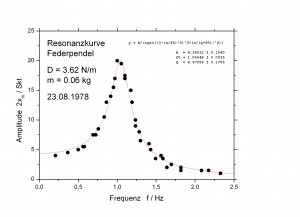Resonanzkurven haben einen gewissen ästhetischen Reiz. Ein Beispiel zeigt die Abbildung. Sie ist das Ergebnis einer Messung an einem Federpendel.

Wir hängen ein Gewichtsstück an eine Schraubenfeder und bewegen das obere Ende der Feder mit der Hand auf und ab. Dabei gerät das Gewichtsstück in Schwingungen. Treffen wir den richtigen Takt beim Auf- und Ab-Bewegen der Feder, schwingt das Gewichtsstück sehr weit aus – wir regen die Schwingung in Resonanz an. Die Resonanzkurve gibt an, wie weit das Federpendel bei verschiedenen Taktfrequenzen ausschlägt. In unserem Fall ist die Schwingungsweite („Amplitude“)  am größten, wenn man die Feder etwa einmal pro Sekunde  auf- und ab bewegt. Das heißt, die Resonanzfrequenz ist 1 Hertz (Hz). Mehr über die Resonanzkurve eines Federpendels.