Nach M. Bauer1 sind die Schüler(innen) der sechsten Klasse davon überzeugt, dass es dumme Brüche gibt. Dumm sind Brüche dann, wenn es schwierig ist herauszufinden, ob und wie man sie kürzen kann. Während man bei 25/75 sofort sieht, dass man mit 25 kürzen kann, braucht man etwas länger, um festzustellen, dass in 391/153 Zähler und Nenner durch 17 teilbar sind. Die Zeit, die man benötigt, um den größten gemeinsamen Teiler (ggT) von Zähler und Nenner zu finden, lässt sich quantitativ angeben als Anzahl der Schritte, die der Euklidische Algorithmus zu seiner Bestimmung erfordert. Mathematisch interessante Fragen, die sich aus dieser Tatsache ergeben, werden in der Arbeit von Bauer1 erörtert.
Fallen alle Körper wirklich gleich schnell?
Galilei ließ Kugeln aus verschiedenem Material zur Erde fallen (der Überlieferung nach vom schiefen Turm zu Pisa) – und stellte fest, dass alle zur gleichen Zeit auf den Boden aufschlugen. Im Physikunterricht kam die Frage auf, wie genau man das mit einfachen Mitteln nachprüfen könne – und in wie weit man dabei den Literaturwert der Fallbeschleunigung (g = 9,81 m/s2) messen würde.
Unsere Körper waren Kugeln mit (fast) gleichem Durchmesser, und zwar ein Tischtennisball (Masse 0,003 kg, Durchmesser 3,8 cm), eine Stahlkugel (Masse 0,229 kg, Durchmesser 3,8 cm) und eine Holzkugel (Masse 0,035 kg, Durchmesser 4,4 cm). Sie durchfielen eine Strecke von ca. 2 m. Ihre Bewegung wurde mit einem Ultraschall-Entfernungsmesser (CBR) gemessen. Dieses Gerät befand sich senkrecht über dem Punkt, an dem die Kugel losgelassen wurde. Das Foto Abb. 1 zeigt den Versuchsaufbau im Treppenhaus der Schule. Der Entfernungsmesser befindet sich am linken Ende der Holzstange. Rechts erkennt man den Datenlogger (TI83). Zur Zeit der Fotoaufnahme werden gerade die Daten des vorhergehenden Versuchs ausgelesen. Deshalb ist die Verbindung zwischen Entfernungsmesser und Datenlogger unterbrochen. Während einer Messung steckt das Kabel des Ultraschallgeräts natürlich in der Eingangsbuchse des Datenloggers.
Primzahlteppiche und Eulers Polynom

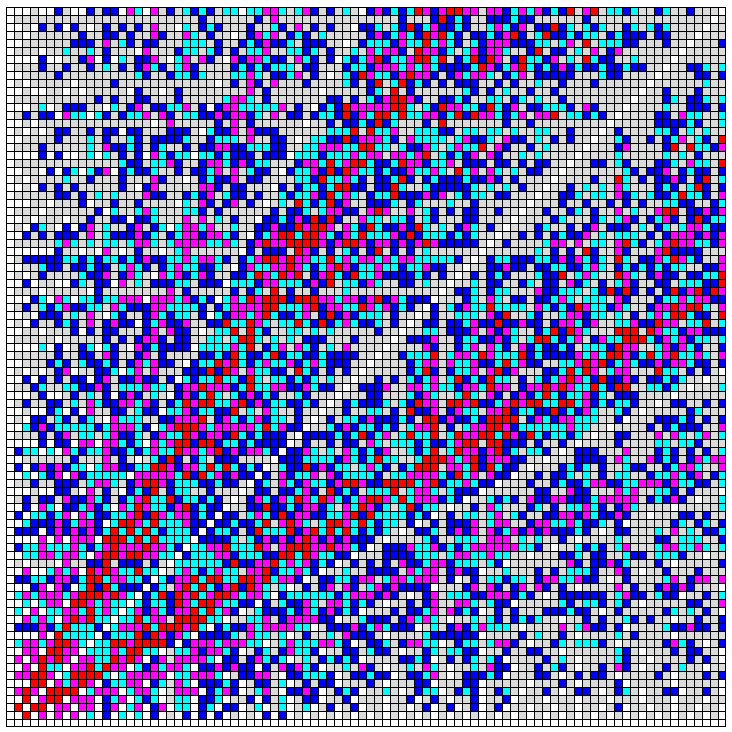
Ein Vorschlag von Bartholomé, Rung und Kern1 aufgegriffen: der Primzahlteppich.
Ein Primzahlteppich ist ein Koordinatengitter, in dem diejenigen Punkte (x, y) markiert werden, für die beispielsweise die Summe x + y, das Produkt xy oder irgendein anderer Rechenausdruck („Term“) T(x, y) eine Primzahl ist. Die Abbildung zeigt den Primzahlteppich des Terms T(x, y) = abs(x – y), das heißt, Punkte bzw. Karos (x, y), für die der Absolutbetrag (abs) der Differenz x – y eine Primzahl ist, sind durch die Farbe weiß gekennzeichnet. Um etwas Farbe in den Teppich zu bringen, markieren wir mit anderen Farben auch die Punkte (Karos), für die der Term eine zusammengesetzte Zahl mit zwei bzw. drei Primfaktoren ist („Fast-Primzahlen“). Wir wählen rot für Zahlen mit zwei Primfaktoren und blau für solche mit drei Primfaktoren. Mehr über Primzahlteppiche hier. Ein Teppich, der die Primzahlen des Eulerschen Polynoms x2 – x + 41 darstellt, ist nochmals an anderer Stelle beschrieben.
1) Bartolomé, Andreas, Josef Rung und Hans Kern: Zahlentheorie für Einsteiger. Vieweg 1995
Schumann-Resonanzen, erster Versuch
 UKW-Rundfunksender arbeiten mit einer Frequenz von etwa 100 MHz. Es gibt aber auch „Radiowellen“ (elektromagnetische Schwingungen) mit sehr viel kleinerer Frequenz. Zum Beispiel 8 Hz – das heißt 8 Schwingungen in einer Sekunde. Sie werden Schumann-Resonanzen genannt, nach W. O. Schumann¹, der sie 1952 aufgrund theoretischer Rechnungen voraussagte.
UKW-Rundfunksender arbeiten mit einer Frequenz von etwa 100 MHz. Es gibt aber auch „Radiowellen“ (elektromagnetische Schwingungen) mit sehr viel kleinerer Frequenz. Zum Beispiel 8 Hz – das heißt 8 Schwingungen in einer Sekunde. Sie werden Schumann-Resonanzen genannt, nach W. O. Schumann¹, der sie 1952 aufgrund theoretischer Rechnungen voraussagte.
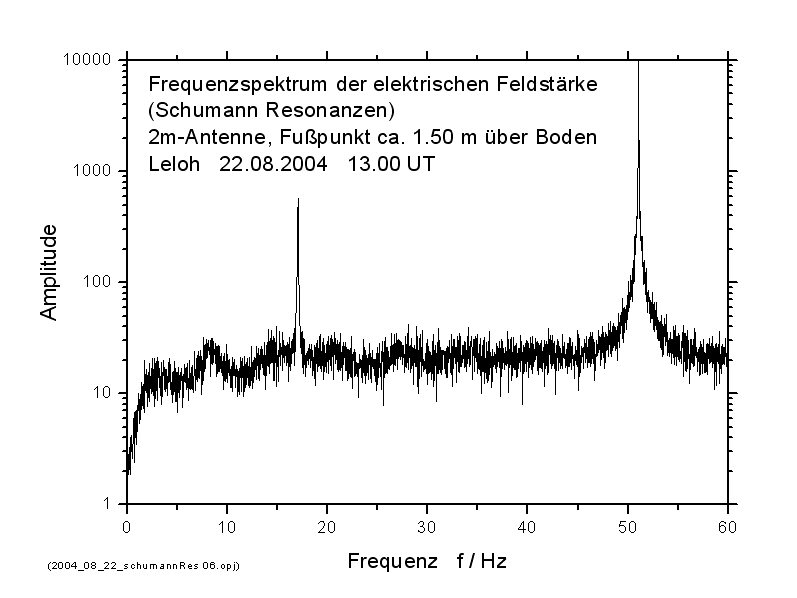
Die Schumann-Resonanzen sind stehende Wellen, die sich zwischen der Erdoberfläche und der Ionosphäre ausbilden. Sie werden durch die Blitze der Gewitter angeregt, die ständig auf der Erde tätig sind. Ihre „Signalstärke“ ist verschwindend klein, ein Empfänger für diese Wellen muss also sehr empfindlich sein. Er ist aber einfach aufzubauen – zumindest dann, wenn es, wie in meinem Fall, nur um den Nachweis der Schumann-Resonanzen geht. Das Foto zeigt einen Probe-Aufbau meines Empfängers und der Antenne. Der Ausgang des Empfängers ist einem PC verbunden, der die „Sendungen“ des Gewitterfunks aufzeichnet. Der zeitliche Verlauf des gespeicherten Signals ist ein Wechselstrom, der sich kaum vom Rauschen eines ohmschen Widerstandes unterscheidet. Mit Hilfe eines FFT-Programms (FFT = Fast Fourier Transform) kann man dennoch feststellen, welche Frequenzen in diesem Signal vorhanden sind und sogar messen, mit welcher relativen Stärke das der Fall ist. Das Diagramm zeigt das Ergebnis der Fourieranalyse: auf einem Untergrund von Rauschen mehrere breite „Buckel“ und zwei scharfe Linien bei 16,7 und 50 Hz. Die breiten Buckel bei 8, 14, 20, 26 und 32 Hz sind die Schumann-Resonanzen, die scharfen Linien entsprechen den Frequenzen des Bahnstroms (16,7 Hz) und der Energieversorgung (50 Hz). Ich gebe zu, die Resonanzen sind nicht sehr ausgeprägt – es ging nur um deren Nachweis, nicht um eine quantitative Messung. Hier mehr über dieses Experiment.
Und auch noch etwas Theorie: Man kann beispielsweise berechnen, bei welchen Frequenzen die Gewitter auf „Sendung“ sind. Die Rechnungen erfordern etwas Mathematik2.
1 W. O. Schumann war Professor für Physik und Direktor des Elektrophysikalischen Instituts der TU München.
2 Die Rechnungen sind Näherungslösungen. Auch diese mathematisch aufwändigere Rechnung ist noch eine Näherung.
Temperatur der Radiosonne bei 10 GHz
 Radioastronomie für Anfänger (wie mich):
Radioastronomie für Anfänger (wie mich):
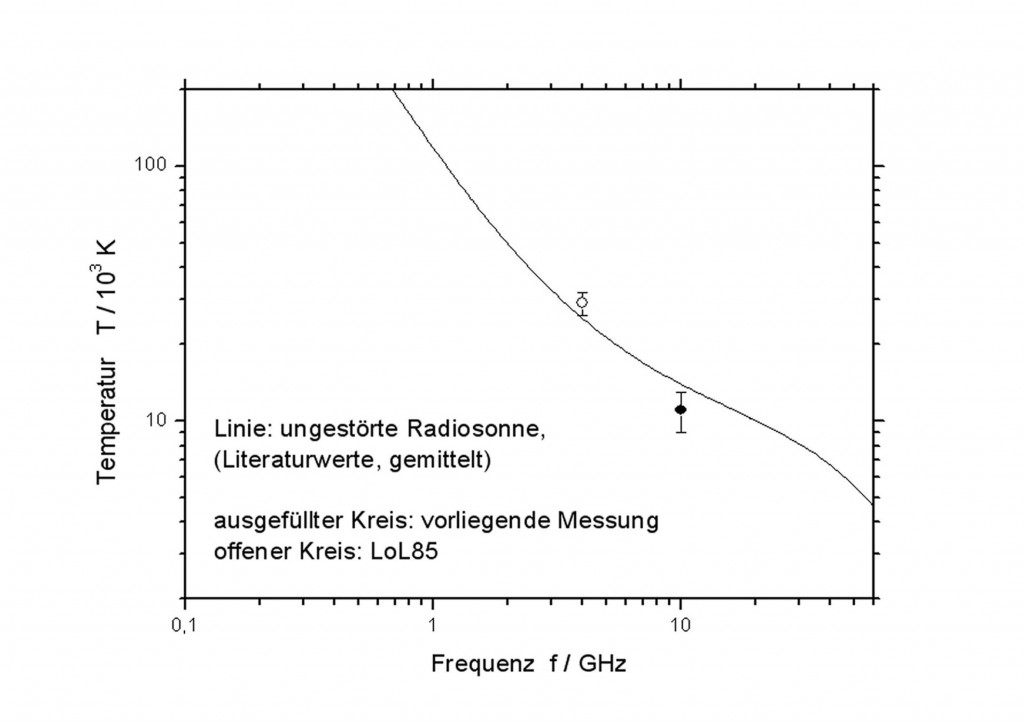
Richtet man eine Satellitenschüssel auf die Sonne, erhöht sich der Rauschpegel am Ausgang des Antennenkonverters (LNC, low noise converter) bezogen auf den Wert, den man normalerweise misst („normalerweise“ bedeutet zum Beispiel, dass die Antennenschüssel auf eine Himmelsregion fernab von der Sonne gerichtet wird). Ein Satellitenortungsgerät (Satfinder) zeigt diesen erhöhten Rauschpegel an. Das Foto zeigt die Messanordnung. Mit diesem „Experiment“ zeigt man, dass die Sonne nicht nur sichtbares Licht, sondern auch Radiostrahlung aussendet – im vorliegenden Experiment Radiostrahlung von ca. 10 GHz. Die Intensität dieser Strahlung gibt man in der Regel an als die Temperatur eines schwarzen Körpers, der mit derselben Intensität strahlt. Durch Vergleich mit der Strahlung einer Hauswand o. ä. kann man die Temperatur der Sonne bei 10 GHz bestimmen. Es sind (11 ± 1) ∙ 103 K (Kelvin). Dieser Wert fügt sich gut in das Diagramm ein, das in der Literatur für die Strahlungsstärke der ruhigen Sonne angegeben wird, siehe die nachfolgende Abbildung. In dieser Abbildung ist auch das Ergebnis einer Messung bei 4 GHz eingetragen, ausgeführt von Studenten im Physik-Praktikum einer Hochschule.
Der von mir bei 10 GHz gemessene Wert 11000 K ist größer als die Temperatur der Sonne im Bereich des sichtbaren Lichts, die 6000 K beträgt. Das deutet darauf hin, dass die Sonne nicht wie ein idealer schwarzer Körper strahlt. Mehr zu diesem Experiment.
Mandelbrot-Menge
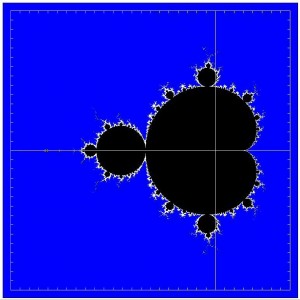
Abb. 1 Abb. 2
Nicht Neues, aber immer wieder interessant: Mandelbrots „Atlas“ der zusammenhängenden Julia-Mengen – genannt „Apfelmännchen“. Die Mandelbrotmenge ist das schwarz gefärbte Gebiet in Abbildung 1. Interessant ist vor allem der Rand der Mandelbrotmenge. Abbildung 2 zeigt ein Beispiel.
CD als Reflexionsgitter
 Eine CD, mit der „Rillenseite“ ins Licht gehalten, erzeugt Farben. Sie entstehen dadurch, dass sich Lichtwellen, die von unterschiedlichen Rillen reflektiert werden, gegenseitig verstärken oder auslöschen – je nach Wellenlänge, Einfallswinkel und Blickrichtung. Dasselbe beobachtet man beim Blick durch ein optisches Gitter. Beim optischen Gitter betrachtet man das hindurchgehende Licht, bei der CD das von ihr reflektierte Licht. Kurzum, die CD müsste sich als Reflexionsgitter eignen. Das ist in der Tat der Fall. Sie in der Schulphysik anstelle von Doppelspalt & Co. einzusetzen bringt auch etwas Schwung in den Unterricht. Das meinte schon einer meiner Kollegen1 und ließ mit einem He-Ne-Laser den genauen Spurenabstand auf der Scheibe messen. Ich drückte meinen Schülern und Schülerinnen eine CD in die Hand mit der Aufgabe, die Wellenlängen einiger Quecksilberlinien zu bestimmen. Das geht recht gut, auch wenn die Formeln, die man zur Auswertung benötigt, etwas unübersichtlich sind. Hier ein Bericht von diesem Experiment.
Eine CD, mit der „Rillenseite“ ins Licht gehalten, erzeugt Farben. Sie entstehen dadurch, dass sich Lichtwellen, die von unterschiedlichen Rillen reflektiert werden, gegenseitig verstärken oder auslöschen – je nach Wellenlänge, Einfallswinkel und Blickrichtung. Dasselbe beobachtet man beim Blick durch ein optisches Gitter. Beim optischen Gitter betrachtet man das hindurchgehende Licht, bei der CD das von ihr reflektierte Licht. Kurzum, die CD müsste sich als Reflexionsgitter eignen. Das ist in der Tat der Fall. Sie in der Schulphysik anstelle von Doppelspalt & Co. einzusetzen bringt auch etwas Schwung in den Unterricht. Das meinte schon einer meiner Kollegen1 und ließ mit einem He-Ne-Laser den genauen Spurenabstand auf der Scheibe messen. Ich drückte meinen Schülern und Schülerinnen eine CD in die Hand mit der Aufgabe, die Wellenlängen einiger Quecksilberlinien zu bestimmen. Das geht recht gut, auch wenn die Formeln, die man zur Auswertung benötigt, etwas unübersichtlich sind. Hier ein Bericht von diesem Experiment.
1 D. Ohlmann, Eine Compact Disk als Versuchsgerät im Physikunterricht, Praxis der Naturwissenschaften – Physik 2/43 (1994).
Zu Boden fallen …
 … viele Gegenstände, zu Boden sinken nur wenige – Luftballons zum Beispiel. Ein Grund dafür, ihr langsames Hinabschweben einmal genauer zu studieren. Das haben die Schüler und Schülerinnen meiner Arbeitsgemeinschaft Physik getan. Einzelheiten dazu hier. Das Versuchsgelände (Foto) war das Treppenhaus unserer Schule.
… viele Gegenstände, zu Boden sinken nur wenige – Luftballons zum Beispiel. Ein Grund dafür, ihr langsames Hinabschweben einmal genauer zu studieren. Das haben die Schüler und Schülerinnen meiner Arbeitsgemeinschaft Physik getan. Einzelheiten dazu hier. Das Versuchsgelände (Foto) war das Treppenhaus unserer Schule.
Foucault-Pendel
Wie zeigt man, dass sich die Erde um ihre Achse dreht – und nicht Sonne, Mond und Sterne die Erde täglich umkreisen? Natürlich mit einem Foucault-Pendel!
Ein spärisches Pendel, das auf der Erdoberfläche in Schwingungen versetzt wird, behält seine Schwingungsebene relativ zu den Fixsternen bei. Währenddessen dreht sich die Erde unter ihm – einmal in 24 Stunden um ihre Achse. Von der Erdoberfläche aus gesehen, dreht sich die Schwingungsebene des Pendels, allerdings nicht um 360 Grad pro Tag, sondern um einen Winkel, der von der geografischen Breite des Pendelortes abhängt. Für eine geografische Breite von 51 Grad nördlich beträgt dieser Winkel 11,7 Grad pro Stunde, wobei die Drehung im Uhrzeigersinn erfolgt.