Nach den Fotos der Baumallee Bassenheim jetzt eine kleine Galerie mit Zeichnungen und Aquarellen, die Bäume, Baumgruppen und Alleen zeigen – angeregt durch die Formen der Bassenheimer Alleebäume.
Goldener Schnitt und Impedanz
Ein „goldenes“ Rechteck
Impedanz ist ein anderes Wort für Wechselstromwiderstand. Es geht also um Elektrotechnik. Um einen Stromkreis, dessen Impedanz von der Frequenz der Stromquelle abhängt. Die Einzelheiten später.
Zunächst zum Goldenen Schnitt: Wir zeichnen ein Rechteck, dessen Länge sich zur Breite verhält wie (√5 + 1)/2 zu 1, oder näherungsweise wie 1,618 zu 1. Spaltet man das größte Quadrat ab, das hineinpasst, bleibt ein Rechteck übrig mit demselben Seitenverhältnis. Aus diesem entfernt man wiederum das größte einbeschriebene Quadrat, und wiederum bleibt ein Rechteck übrig, dessen Seitenlängen sich wie (√5 + 1)/2 zu 1 verhalten. Das Spiel lässt sich ad infinitum fortsetzen – aber nur dann, wenn man wie oben mit dem genannten Seitenverhältnis beginnt. In der Abbildung sind die ersten Schritte erkennbar. Die Zahlen (√5 + 1)/2 = 1,618339… und (√5 – 1)/2 = 0,618339… , die hier eine Rolle spielen, sind die Teilungsverhältnisse des Goldenen Schnitts. In der Kunst soll er besonders angenehme Proportionen erzeugen. Dass er auch in anderen Bereichen „mitmischt“, ist bekannt.
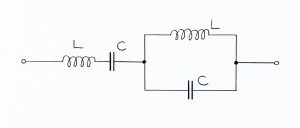
Ein Beispiel aus der Elektrotechnik ist der nachfolgende Wechselstromkreis. Seine Impedanz
Stromlaufplan unserer Schaltung
(sein Wechselstromwiderstand) ist Null für zwei Kreisfrequenzen, die durch die Resonanzfrequenz 1/√LC der Einzelkreise im Verhältnis des Goldenen Schnitts geteilt wird. Mehr
Schreibtischexperiment: c nach Römer
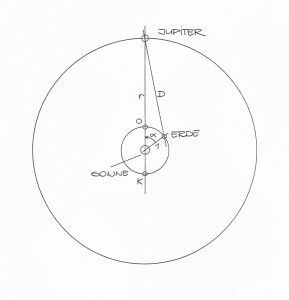
Abbildung: Bahnen von Erde und Jupiter und Bestimmung der Entfernung Jupiter-Erde. O: Jupiter in Opposition zur Sonne (nachts), K: Jupiter in Konjunktion zur Sonne (am Tage). Entfernungen in astronomischer Einheit AE (1 AE = 149,6 Millionen km)
Ein geniales „Experiment“, am Schreibtisch nachempfunden: Ole Rømers Bestimmung der Lichtgeschwindigkeit.
Zuvor einige Erläuterungen zu Messmethode: Schon Galilei richtete nachts sein Fernrohr auf den Planeten Jupiter und stellte fest, das dieser von Monden umkreist wird. Damit waren Jupiter und seine Monde das erste System, an dem man durch Beobachtung von „Außen“ die Bewegung von Satelliten studieren konnte. Ole Rømer untersuchte das Kreisen der Jupitermonde genauer. Und prompt entdeckte er, dass einer der Monde, nämlich Io, es mit den Gesetzen der Physik offenbar nicht so genau hielt: Seine beobachtete Umlaufzeit wurde größer, je weiter sich die Erde vom Jupiter und damit von ihm, dem Mond Io, entfernte. Wie kommt es dazu?
Die (synodische) Umlaufzeit des Jupitermondes Io beträgt TIo = 1,76986 Tage (d). Dies ist die Zeitspanne, die beispielsweise verstreicht zwischen zwei aufeinanderfolgenden Austritten dieses Mondes aus dem Kernschatten des Jupiters (Verfinsterungsende). Rømer bestimmte die Zeitpunkte der Verfinsterungsenden über längere Zeit hinweg. Um seine Vorgehensweise nachzuvollziehen, nehmen wir an, dass Jupiter am Anfang seiner Beobachtungsreihe in Opposition zur Sonne stand. Die Erde befindet sich dabei im Punkt O der Abbildung, so dass die Entfernung zwischen Jupiter und Erde minimal war. In der Folgezeit nahm der Abstand zwischen Erde und Jupiter fortlaufend zu, da sich die Erde in Richtung Konjunktionsstellung (Punkt K in der Abbildung) bewegte, während Jupiter wegen seiner 12-jährigen Umlaufzeit praktisch auf der Stelle trat. Rømer stellte fest, dass die Verfinsterungsenden im Laufe der Zeit immer später eintrafen als vorherberechnet. Das heißt, das Verfinsterungsende nach beispielsweise 90 Io-Umläufen trat nicht genau 90 ×1,76986 Tage später ein als das erste von ihm beobachtete Verfinsterungsende, sondern hinkte einige Minuten hinterher. Er zog daraus den richtigen Schluss, dass diese Verzögerung der Zeitdauer entspricht, die das Licht benötigt, um die Entfernungsdifferenz zwischen den Positionen der Erde am Anfang und Ende der Beobachtungsreihe zurückzulegen.
Verzögerung und Entfernungsdifferenz lassen sich aus Ephemeridentabellen bzw. astronomischen Tafelwerken ermitteln. Die Rechnung ergibt beispielsweise, dass für eine Entfernungsdifferenz von 150,1 Millionen Kilometern die Verzögerung 9,28 Minuten = 557,1 Sekunden beträgt. Daraus folgt für die Lichtgeschwindigkeit ein Wert von c = 269500 km/s. Nimmt man an, dass die Verzögerung auf etwa ± 2 Minuten genau bestimmt werden kann, ergibt sich für die Lichtgeschwindigkeit einschließlich Fehler c = (269500 ± 58100) km/s. Dieser Wert ist innerhalb der Fehlergrenzen mit dem Literaturwert c = 299792,458 km/s verträglich.
Aquarelle – Übungen in Lasurtechnik
Auf dem Übungsprogramm steht zur Zeit die Lasurtechnik. Hier erste Ergebnisse, noch verbesserungsbedürftig.
Ulams Primzahlspirale
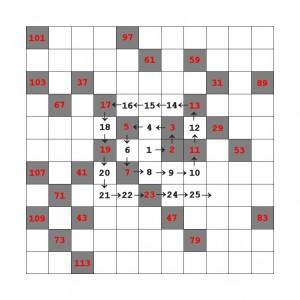
Ulams (viereckige) Primzahlspirale. Die natürlichen Zahlen werden, in der Mitte mit 1 beginnend, der Reihe nach spiralförmig im Gegenuhrzeigersinn eingetragen. Hier sind es die Zahlen bis einschließlich 121 in der rechten unteren Ecke.
Wir nehmen ein Blatt kariertes Papier zur Hand und tragen die natürlichen Zahlen der Reihe nach in die Karos ein. Den Anfang macht die 1 in der Mitte des Blattes. Rechts davon wird die 2 platziert, im Kästchen darüber die 3 und links davon die beiden Zahlen 4 und 5. Die 6 und 7 belegen die Karos unterhalb der 5, und die 8 wird rechts von der 7 eingetragen, usw. Das heißt, wir bewegen uns im Gegenuhrzeigersinn auf einer (viereckigen) Spirale nach außen. Geraten wir an eine Primzahl, wird das zugehörige Kästchen farbig markiert.
Das Ergebnis sollte dann aussehen wie in der Abbildung.
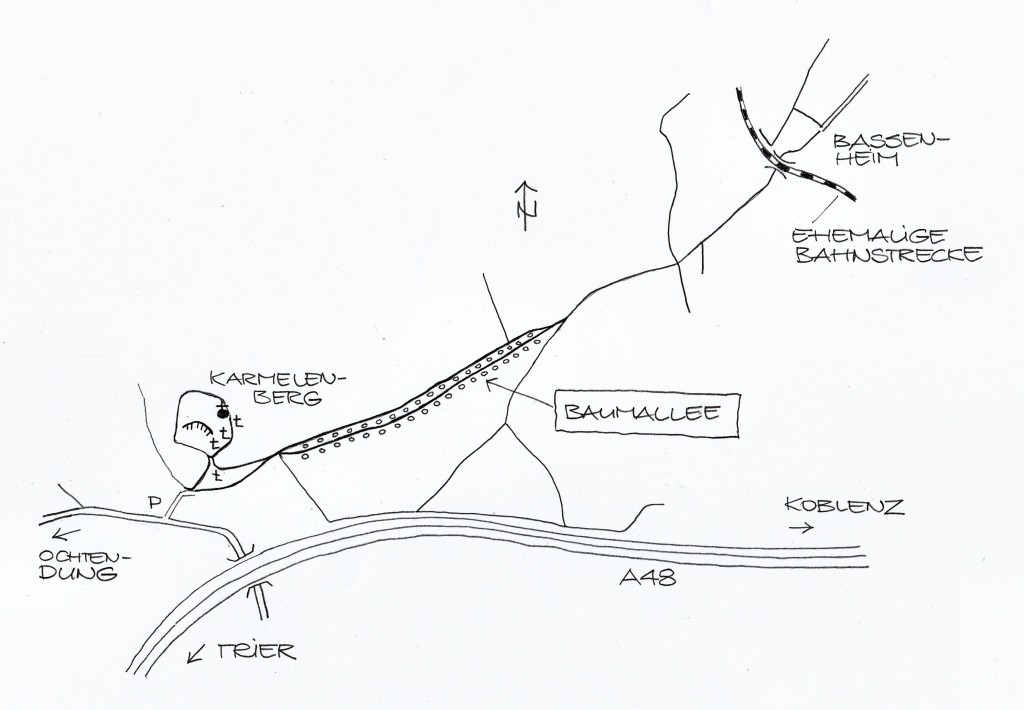
Naturdenkmal Baumallee Bassenheim
Bassenheim ist ein linksrheinischer Ort in der Nähe von Koblenz. Von dort geht in Richtung Westen ein Fußweg zu einem alten Vulkankegel, auf der Karte als „Karmelenberg“ bezeichnet. Der Weg unterquert den Viadukt einer stillgelegten Eisenbahnstrecke, durchläuft ein kurzes Stück Wald und mündet dann in eine Allee von zum Teil uralten Bäumen – ein faszinierender Anblick. Die Fotos sind keine Meisterwerke – beiläufig aufgenommen beim Wandern auf dem Rheinburgenweg. Der etwas seltsam anmutende Name „Karmelenberg“ leitet sich her, wie man liest, vom Berg Karmel im Norden Israels. Im Alten Testament wird berichtet, dass Elia dort das Gottesurteil gegen die Propheten des Baal herbeiführte (1. Kön 18). Offenbar gibt es noch mehr Stätten, die nach dem Berg in Israel benannt sind. Zum Beispiel der Ort Carmel-by-the-Sea (bei Monterey, Californien, USA) und die dortige Missionsstation Carmel Mission.
Perfektes Quadrat
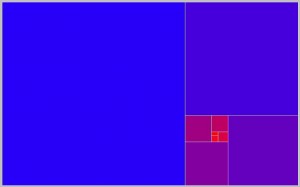
Ein Quadrat ist ein rechtwinkliges Viereck mit vier gleich langen Seiten. Ein perfektes Quadrat ist ein Quadrat, das sich vollständig in kleinere Quadrate aufteilen lässt, wobei keine zwei dieser Teilquadrate einander gleich sein dürfen – oder, etwas mathematischer formuliert: Ein Quadrat, das sich in lauter paarweise verschieden große Quadrate zerlegen lässt, heißt perfekt.
Die Abbildung zeigt Exemplare des perfekten Quadrats der Ordnung 21. Es enthält 21 paarweise verschiedene Teilquadrate – mit unterschiedlichen Farben ausgemalt. Mehr…
Wandern auf dem Rheinburgenweg
Eine kleine Sammlung von Fotos vom linksrheinischen Rheinburgenweg zwischen Bingen und Mehlem. Auch hier war ich in einzelnen Tagesetappen unterwegs. Ein Highlight: der Blick auf die Loreley vom Aussichtspunkt Maria Ruh.
Galerie von Feigenbaum-Diagrammen
Mit Botanik haben Feigenbaum-Diagramme nichts zu tun. Es geht hier um Mathematik. Von Feigenbaum-Diagrammen war schon einmal die Rede, auch von der Mathematik, die diesen Gebilden zugrunde liegt. Heute eine kleine Galerie von (hoffentlich) interessanten Diagrammen.
Die nachfolgende Einführung erklärt kurz, worum es geht.
Rheinsteig – 300 Kilometer Wanderlust
Nach 14 Tagesetappen, verteilt über zwei Jahre, hatte ich den Abschnitt zwischen Wiesbaden und Königswinter komplett zurückgelegt. Laut GPS-Gerät war das, einschließlich der Verbindungswege von und zu den Bahnhöfen entlang des Rheins, eine Strecke von etwa 300 Kilometern, mit Anstiegen von insgesamt 8500 Höhenmetern (daher offenbar der Name „Steig“).
Zur Dokumentation einige Fotos: Stimmungsbilder, im Vorübergehen gemacht. Sicher nicht die Highlights des Steigs. Das obige zeigt Bacharach.
