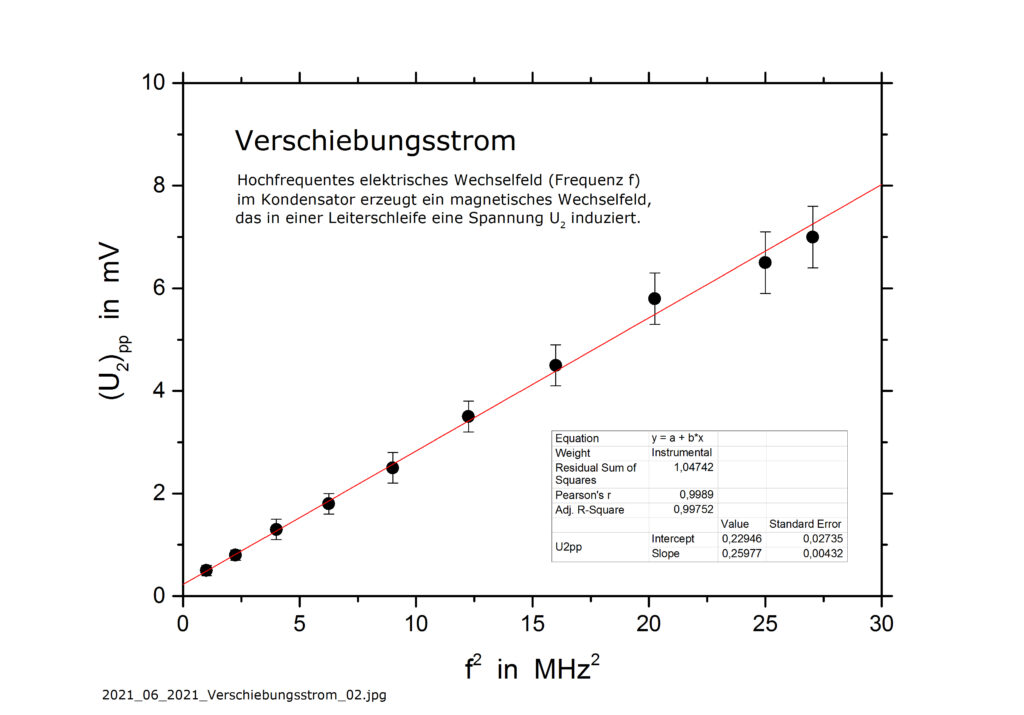
Vom Kriegerdenkmal auf dem Klever Springenberg sieht man bei gutem Wetter, durch eine Schneise im Wald blickend, am fernen Horizont den Kirchturm von St. Vitus in Hoch-Elten. In der Sichtlinie zur Kirche liegt im Vordergrund das von Bäumen gesäumte Wasserbecken eines Kanals, den Johann-Moritz von Nassau-Siegen seinerzeit anlegen ließ.
Schaut man etwas genauer hin, bemerkt man, dass sich die Fluchtlinien der Kanalufer und die der Baumreihen links und rechts des Wasserbeckens am Ort der Eltener Kirche treffen – eine, wie man liest, von Johann-Moritz gewollte Landschaftsgestaltung in Form einer Sichtachse. Für mich eine Gelegenheit, mein Java-Programm Zentralperspektive nochmals zu testen. Einen ersten Test hatte es schon bestanden: Der Blick in eine abschüssige und in der Ferne wieder ansteigende Straße in San Francisco wurde perspektivisch richtig wiedergegeben. Im vorliegenden Fall ist die Situation ähnlich. Das Gelände längs der Sichtlinie fällt zunächst ab, verläuft dann im Bereich des Kanals und der Rheinebene in der Horizontalen, und steigt erst nach mehreren Kilometern bis auf die Höhe des Eltener Berges wieder an.
Zum Test lasse ich das Programm die perspektivische Ansicht des Kanals und die der Baumreihen links und rechts des Kanals berechnen – und, unabhängig davon, die Lage des Bildpunktes der Eltener Kirche. Der Kanal wird durch ein langgezogenes Rechteck angenähert, mit zur Sichtlinie parallelen Längsseiten.
Das Program m benötigt als Eingabedaten die Eckpunkte des Kanal-Rechtecks und die Lage der Kirche in der realen Welt. Es verarbeitet die Daten nach den Gesetzen der Zentralperspektive und gibt die folgenden, in das nebenstehende Foto hineinkopierten geometrischen Gebilde aus: die Umrisse des Kanals (ein zum Trapez perspektivisch verkürztes Rechteck), die Linien der Baumreihen links und rechts des Kanals und die Lage des Bildpunktes der Eltener Kirche (rotes Kreuz). Die horizontale blaue Linie kennzeichnet die Höhe, in der sich der Wasserspiegel des Rheins befinden müsste. Die in das Foto zusätzlich hineinkopierten grünen Linien sind die Achsen eines Koordinatensystems, deren Schnittpunkt der Durchstoßpunkt der Sichtlinie durch die Bildebene ist (Augenpunkt). Die horizontale Achse dieses Systems ist der Horizont.
m benötigt als Eingabedaten die Eckpunkte des Kanal-Rechtecks und die Lage der Kirche in der realen Welt. Es verarbeitet die Daten nach den Gesetzen der Zentralperspektive und gibt die folgenden, in das nebenstehende Foto hineinkopierten geometrischen Gebilde aus: die Umrisse des Kanals (ein zum Trapez perspektivisch verkürztes Rechteck), die Linien der Baumreihen links und rechts des Kanals und die Lage des Bildpunktes der Eltener Kirche (rotes Kreuz). Die horizontale blaue Linie kennzeichnet die Höhe, in der sich der Wasserspiegel des Rheins befinden müsste. Die in das Foto zusätzlich hineinkopierten grünen Linien sind die Achsen eines Koordinatensystems, deren Schnittpunkt der Durchstoßpunkt der Sichtlinie durch die Bildebene ist (Augenpunkt). Die horizontale Achse dieses Systems ist der Horizont.
Die Längsseiten des Kanal-Rechtecks und die Linien der Baumreihen werden verlängert und treffen sich in einem gemeinsamen Fluchtpunkt. Dieser liegt, da die Linien in der realen Welt parallel zur Blickrichtung und horizontal verlaufen, im Augenpunkt auf dem Horizont. Wie zu erwarten liegt dort, zumindest in grober Näherung, auch der Bildpunkt der Eltener Kirche (rotes Kreuz). Genau genommen liegt der Bildpunkt auf der Senkrechten durch den Augenpunkt, und zwar minimal (und daher kaum erkennbar) oberhalb des Horizonts, da die Kirche in der realen Welt einige Höhenmeter mehr als der Kamera-Standort aufweist.
Das Foto zeigt im Übrigen, dass der Kamera-Standort in horizontaler Richtung nicht exakt in Kanalmitte liegt. Der Kanal wurde deshalb etwas weiter nach links verschoben (durch Änderung der X-Koordinaten seiner Eckpunkte). Berechnung und Foto stimmten danach besser überein, exakte Deckungsgleichheit ließ sich nicht herstellen. Die (kleine) Korrektur äußert sich in der seitlichen Verschiebung der vertikalen grünen Koordinatenachse gegenüber der Mitte des Kanals – und gegenüber der Statue vorne im Bild (Balkenhols »Neuer Eiserner Mann«).
Insgesamt betrachtet, gibt es zwar kleine Abweichungen zwischen Theorie und Praxis, beispielsweise zwischen dem im Foto abgebildeten und dem theoretisch berechneten Kanalufer. Aber abgesehen davon wird die reale Welt durch das Programm richtig in die Bildebene transformiert. Das Programm hat einen weiteren Test bestanden. Eine ausführlichere Beschreibung des Tests hier.
Es gibt im Übrigen in Kleve weitere Schneisen, Wege und Alleen, die auf markante Bauwerke oder Landschaftspunkte ausgerichtet sind, beispielsweise die „Galleien“ in der Ebene des Kermisdal-Bogens. Sie wurden auch von Johann-Moritz angelegt.