Mit Botanik haben Feigenbaum-Diagramme nichts zu tun. Es geht hier um Mathematik. Von Feigenbaum-Diagrammen war schon einmal die Rede, auch von der Mathematik, die diesen Gebilden zugrunde liegt. Heute eine kleine Galerie von (hoffentlich) interessanten Diagrammen.
Die nachfolgende Einführung erklärt kurz, worum es geht.
Die Zahlenfolge 1, 1, 2, 3, 5, 8, 13, 21, … ist vielleicht bekannt. Man startet mit der 1 (Eins), fügt noch eine 1 (Eins) hinzu, und bildet das nächste Folgeglied, indem man beide addiert. Das ergibt die 2 an der dritten Stelle. Die nachfolgende 3 ist die Summe aus dem Vorgänger 2 und dem Vor-Vorgänger 1. Und nach diesem Verfahren findet man alle weiteren Zahlen der Folge: Die Zahl xn+1 an der n +1-ten Stelle ist die Summe aus der vorherigen Zahl xn und der vorvorherigen Zahl xn-1. In mathematischer Kurzschrift notiert, heißt das xn+1 = xn + xn-1. Die Folge ist übrigens nach dem italienischen Mathematiker Fibonacci benannt.
Jedes Folgeglied entsteht durch Rückgriff oder Rekursion auf schon berechnete Folgeglieder. Weil in der Fibonacci-Folge jedes Folgeglied nicht nur aus dem Vorgänger, sondern auch aus dem Vor-Vorgänger berechnet wird, spricht man von einer zweistufigen Rekursion. Wir erweitern und verändern die Rekursionsvorschrift xn+1 = xn + xn-1, indem wir nicht auf xn, sondern auf dessen Quadrat xn2 zurückgreifen, das xn-1 mit einem Minuszeichen versehen und schließlich noch eine (reelle) Konstante c hinzuaddieren. Das führt zu der Rekursionsformel xn+1 = xn2 – xn-1 + c.
Jetzt wird gerechnet. Welche Zahlen durchläuft die Folge für beispielsweise c = – 2, wenn wir, wie bei Fibonacci, mit einer 1 auf den ersten beiden Plätzen starten? Es sind die Zahlen 1, 1, – 2, 1, 1, – – 2, 1, 1, – 2, … , eine sich wiederholende Folge mit dem Zyklus [1, 1, – 2]. Für c = 0 erhält man 1, 1, 0, – 1, 1, 2, 3, 7, 46, 2109, …. Diese Folge wächst über alle Grenzen – sie divergiert, wie man sagt. Setzt man c = 0.5, ergibt sich die Folge 1, 1, 0.5, – 0.25, 0.0625, 0.7539, 1.0058, …, wobei die beiden letzten Zahlen Näherungswerte sind. Diese Folge verhält sich etwas „sprunghaft“, gewissermaßen chaotisch, bleibt aber beschränkt.
Die Beispiele zeigen: Das Verhalten der Folgen ist abhängig vom Wert von c. Das lässt sich in einem x-y-Koordinatensystem demonstrieren. Man trägt dazu die Werte xn der Folge in y-Richtung auf, und zwar über der Stelle, an der in x-Richtung das zur Folge gehörende c steht. Meist trägt man nicht alle Folgewerte auf, sondern nur die ab einer bestimmten Platznummer n. Eine solche „Endzustandsübersicht“ wird Feigenbaum-Diagramm genannt. Feigenbaum ist ein amerikanischer Mathematiker, der diese Art der Darstellung zum ersten Mal benutzt hat, und zwar bei der Untersuchung der Rekursion xn+1 = xn2 + c.
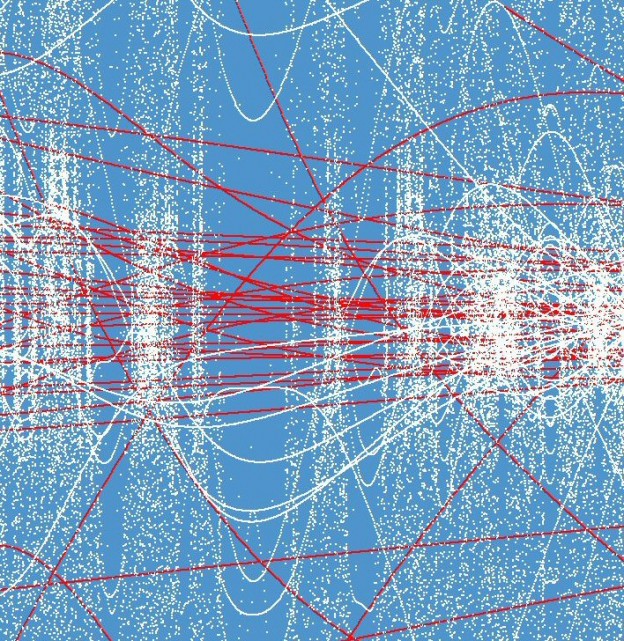
Feigenbaum-Diagramm, siehe Text
Feigenbaum-Diagramme haben einen gewissen ästhetischen Reiz – vor allem, wenn man den Punkten je nach ihrer Platznummer verschieden Farben gibt. Meist beschränkt man sich auch auf kleine Ausschnitte des Koordinatensystems. Die Abbildung zeigt beispielsweise Folgewerte, die bei der Rekursion xn+1 = xn2 – xn-1 + c entstehen, und zwar im Intervall zwischen xn = 0,99 und xn = 1,01 (y-Richtung), und für Parameterwerte c zwischen c = 0,28400 und c = 0,28408 (x-Richtung). Punkte mit Platznummern n zwischen 100 und 500 sind rot, diejenigen mit Nummern zwischen 500 und 2000 sind weiß gefärbt. Man beachte das Chaos der weißen Punkte.