Schrittzahl beim Euklidischen Algorithmus, siehe Text
Nach M. Bauer1 sind die Schüler(innen) der sechsten Klasse davon überzeugt, dass es dumme Brüche gibt. Dumm sind Brüche dann, wenn es schwierig ist herauszufinden, ob und wie man sie kürzen kann. Während man bei 25/75 sofort sieht, dass man mit 25 kürzen kann, braucht man etwas länger, um festzustellen, dass in 391/153 Zähler und Nenner durch 17 teilbar sind. Die Zeit, die man benötigt, um den größten gemeinsamen Teiler (ggT) von Zähler und Nenner zu finden, lässt sich quantitativ angeben als Anzahl der Schritte, die der Euklidische Algorithmus zu seiner Bestimmung erfordert. Mathematisch interessante Fragen, die sich aus dieser Tatsache ergeben, werden in der Arbeit von Bauer1 erörtert.
Euklidischer Algorithmus: Sind x und y zwei Zahlen, deren ggT bestimmt werden soll und für die gilt x > y, so bilde die Differenz x – y. Du hast damit eine dritte Zahl gefunden, die den gesuchten Teiler enthält. Statt den ggT von x und y zu suchen, bestimme jetzt den ggT der beiden Zahlen y und x – y. Setze dieses Verfahren solange fort, bis eine der Zahlen Null ist. Die von Null verschiedene Zahl des letzten Paares ist der gesuchte ggT.
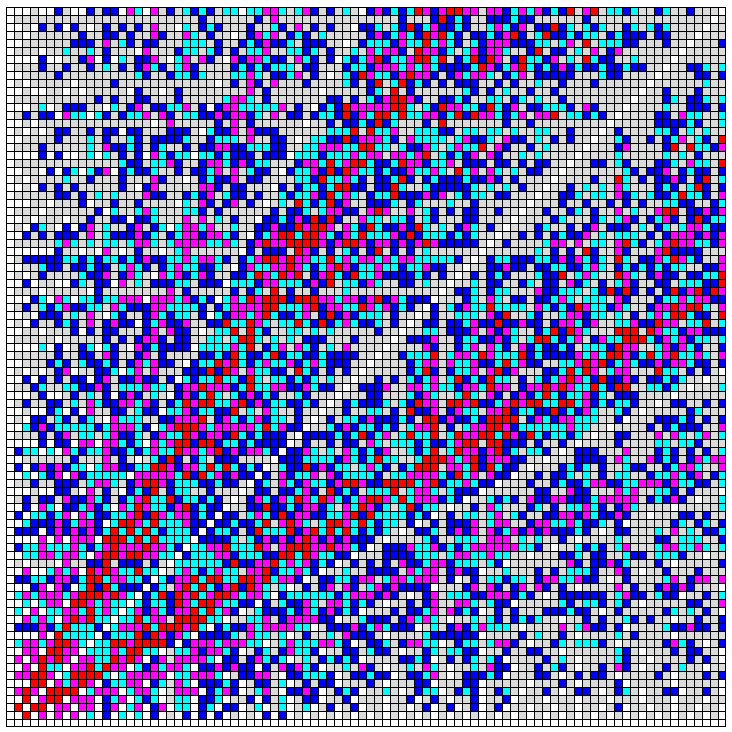
Der Euklidische Algorithmus ist in der Tat faszinierend – und die Darstellung der Schrittzahl in einem Koordinatensystem führt zu einer eindrucksvollen Grafik. Hier mein Versuch einer solchen Darstellung: Die Abbildung zeigt die Schrittzahl, die zur Bestimmung des ggT(x,y) nach Euklid benötigt wird, als Funktion von x und y. Jedes Karo repräsentiert ein Zahlenpaar (x,y) und ist entsprechend der relativen Schrittzahl gefärbt. Da der ggT symmetrisch in x und y ist – es gilt ggT(x,y) = ggT(y,x), wird das Muster der Karos unterhalb der Winkelhalbierenden an dieser nach oben gespiegelt. Karos von Paaren mit maximaler Schrittzahl sind rot gefärbt, solche mit der um eins, zwei oder drei gegenüber der Höchstzahl verminderten Schrittzahl magenta, cyan bzw. blau. Alle Karos, die Paaren mit noch kleinerer Schrittzahl entsprechen, erscheinen grau – bis auf diejenigen, die nur einen einzigen Schritt erfordern, sie wurden weiß gefärbt. Viele Paare maximaler Schrittzahl (rote Karos) liegen in etwa in der Nähe der Geraden x = 0,618 y bzw. y = 0,618 x (0,618 ist das Verhältnis der kleineren zur größeren Strecke beim Goldenen Schnitt). Es gibt jedoch Paare deutlich oberhalb dieser Geraden. Auch die magentafarbenen Karos (Schrittzahl um eins kleiner als die maximale Schrittzahl) gruppieren sich in der Nähe von Geraden, zum Beispiel x = 3y/8 (bzw. y = 3x/8). Die durch die weißen Karos angedeuteten Geraden entsprechen den Gleichungen x = y/2 (y = x/2), x = y/3 (y = x/3), usw. In diesen Fällen ist x (y) die Hälfte, ein Drittel, usw. von y (x), so dass der Algorithmus nur einen Schritt benötigt. Mehr zum Euklidischen Algorithmus hier.
1 Bauer, M.: Die dümmsten Brüche und die blödesten Nenner, mathe-plus 2, (1), S. 12 (1985)