Daniel Kehlmann beschreibt die Szene in seinem Buch „Die Vermessung der Welt” mit hintergründigem Humor: Carl Friedrich Gauß und Alexander von Humboldt unterhalten sich über das Magnetfeld der Erde. Humboldt brüstet sich damit, mehr als zehntausend Messungen des Feldes gemacht zu haben. Gauß entgegnet cool, Daten heranschleppen reiche nicht, man müsse auch denken – und lässt „leise lachend” die Bemerkung fallen: „Einfache Kugelfunktionen”. Weiter heißt es dann: „Kugelfunktionen. Humboldt lächelte. Er hatte kein Wort verstanden.”
Kugelfunktionen sind für mich nicht das Problem, aber was Gauß mit „denken” meint, war mir dann doch nicht so ganz klar. Also Literaturstudium. Was mir zum Verständnis wichtig erschien, habe ich hier zusammengestellt.
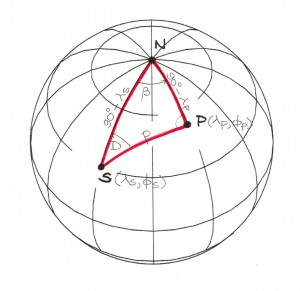
Gauß stellte die Magnetfeldstärke als Summe von Kugelfunktionen dar und bestimmte die Anteile der einzelnen Summanden so, dass die damaligen Messwerte (zum Beispiel die von Humboldt) richtig wiedergegeben wurden. Das macht man auch heute noch so – mit den aktuellen Messwerten. Dabei ergibt sich, dass eine einzige Kugelfunktion in dieser Summe überwiegt. Sie beschreibt ein Feld, das außerhalb der Erde wie das eines gigantischen Stabmagneten aussieht (ein Dipolfeld). In diesem Feld gibt es zwei gegenüberliegende Orte auf der Erde, an denen die magnetischen Feldlinien senkrecht aus der Erde austreten bzw. wieder eintreten: die magnetischen Pole. Da man den Verlauf der Feldlinien kennt, kann man aus den Messwerten von Deklination und Inklination an einem beliebigen Ort der Erde die Position des magnetischen Nord- bzw. Südpols näherungsweise errechnen. Die Abbildung zeigt, dass man dazu etwas sphärische Trigonometrie benötigt. Mehr dazu steht auch hier.