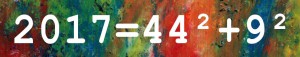2017 – nach sechs Jahren endlich wieder eine Primzahl. 2011 war das letzte Primzahljahr, das nächste ist 2027, also erst 10 Jahre später. Primzahlen sind nur durch 1 und sich selbst teilbar. Sie weigern sich, in ein Produkt zerlegt zu werden, sind aber gerne bereit, als Faktoren in normalen Zahlen aufzutreten. Die Zahl 60 zum Beispiel ist gleich dem Produkt 2²×3×5 der Primzahlen 2, 3 und 5.
Dass 2017 eine Primzahl ist, regt uns nicht auf. Schließlich gibt es unendlich viele davon, das wusste schon Euklid – und konnte es auch beweisen. Das Besondere an 2017 ist, dass die Zahl bei Division durch 4 den Rest 1 übrig lässt (2017 = 4×504 + 1). Nur Primzahlen mit dieser Eigenschaft lassen sich in eine Summe von genau zwei Quadratzahlen zerlegen – nach Fermat’s berühmtem Zwei-Quadrate-Satz1. Der Satz gilt für alle Primzahlen größer als 2. Beispiele: 5 = 2² + 1², 13 = 3² + 2², 17 = 4² + 1². In unserem Fall ist 2017 = 44² + 9². Also notieren wir:
| 2017 ist eine Primzahl, die durch 4 geteilt, den Rest 1 ergibt. Sie lässt sich daher als Summe von 2 Quadraten schreiben: 2017 = 44² + 9² (Zwei-Quadrate-Satz von Fermat). |
Weitere Besonderheiten von 2017 als Primzahl tun sich auf, wenn man die Zahl in den Nenner eines (echten) Bruches schreibt, zum Beispiel 1/2017. Brüche, deren Nenner eine Primzahl ist, sind in Kommaschreibweise rein periodische Dezimalbrüche. Die Anzahl der sich wiederholenden Dezimalstellen heißt Periodenlänge. Der Zähler des Bruchs hat keinen Einfluss auf die Periodenlänge. Zwei Beispiele: 1/3 = 0,333333… hat eine Periode der Länge 1, 1/7 = 0,142857142857…. eine Periode der Länge 6. Beim Nenner 7 hat die Periode die maximal mögliche Länge. Denn beim (schriftlichen) Dividieren durch 7 gibt es höchstens 6 verschiedene Reste, die maximal mögliche Länge ist also der um 1 verminderte Nenner. Nicht alle Primzahl-Nenner erzeugen Perioden größtmöglicher Länge. Von den 45 Primzahlen kleiner als 200 sind es genau 14, also etwa 30%. Dezimaldarstellungen mit maximal möglicher Periodenlänge sind also nicht die Regel.
Für Brüche mit der Primzahl p als Nenner ist die Periodenlänge die kleinstmögliche Zahl m, für die 10m geteilt durch p den Rest 1 ergibt. Im Fall p = 7 erhält man
101/7 = 1 Rest 3
102/7 = 14 Rest 2
103/7 = 142 Rest 6
104/7 = 1428 Rest 4
105/7 = 14285 Rest 5
106/7 = 142857 Rest 1
Der kleinstmögliche Exponent m, der bei Division von 10m durch 7 den Rest 1 ergibt, ist demnach 6, in Übereinstimmung mit 1/7 = 0,142857142857… . Für den Nenner 2017 ist die Periodenlänge ebenfalls maximal, also 2016. Wir halten also als zweite Besonderheit von 2017 fest:
| Der Bruch 1/2017 hat, als Dezimalzahl geschrieben, die maximal mögliche Periodenlänge von 2016 Stellen. 2016 ist der kleinste Exponent m, der bei Division von 10m durch 2017 den Rest 1 übrig lässt. |
Damit haben wir immerhin zwei bemerkenswerte Eigenschaften der Zahl 2017 festgestellt. Für diejenigen, die es genau wissen wollen: Die ersten 2200 Dezimalen von 1/2017 lauten
0.00049578582052553296975706494794248884481903817550818046603867\
1294000991571641051065939514129895884977689638076351016360\
9320773425880019831432821021318790282597917699553792761527\
0203272186415468517600396628656420426375805651958353991075\
8552305404065443728309370352007932573128408527516113039167\
0798215171046108081308874566187407040158651462568170550322\
2607833415964303420922161626177491323748140803173029251363\
4110064452156668319286068418443232523549826474962816063460\
5850272682201289043133366385721368368864650470996529499256\
3212692117005453644025780862667327714427367377293009419930\
5899851264253842340109072880515617253346554288547347545860\
1883986117997025285076846802181457610312345066931085770946\
9509172037679722359940505701536936043629152206246901338621\
7154189390183440753594447198810114030738720872583044124938\
0267724343083787803668815071888943976202280614774417451660\
8824987605354486861675756073376301437778879524045612295488\
3490332176499752107089737233515121467526028755577590480912\
2459097669806643529995042141794744670302429350520575111551\
8096182449181953396132870599900842835894893406048587010411\
5022310361923648983639067922657411998016856717897868120971\
7402082300446207238472979672781358453148239960337134357957\
3624194348041646008924144769459593455627169062964799206742\
6871591472483886960832920178482895389191869112543381259295\
9841348537431829449677739216658403569657907783837382250867\
6251859196826970748636588993554784333168071393158155676747\
6450173525037183936539414972731779871095686663361427863163\
1135349529003470500743678730788299454635597421913733267228\
5572632622706990580069410014873574615765989092711948438274\
6653445711452652454139811601388200297471492315319781854238\
9687654933068914229053049082796232027764005949429846306395\
6370847793753098661378284581060981655924640555280118988596\
9261279127416955875061973227565691621219633118492811105602\
3797719385225582548339117501239464551313832424392662369856\
2221120475954387704511650966782350024789291026276648487853\
2473971244422409519087754090233019335647000495785820525532\
9697570649479424888448190381755081804660386712940009915716\
4105106593951412989588497768963807635101636093207734258800\
19831432821021318790282597917699553792761527020327219
Wer sich nicht von dem Wust an Ziffern abschrecken lässt, erkennt in der viertletzten Zeile den Beginn der zweiten Periode (Ziffernfolge 000495785…).
1 Die Beweisidee des 2-Quadrate-Satzes hat Ian Stewart in eine humorvolle Nacherzählung von Charles Dickens’ „Weihnachtslied in Prosa“ („A Christmas Carol in Prose“) eingebaut: Ian Stewart „Ein Weihnachtslied in Prosa“, Spektrum der Wissenschaft, Digest: Mathematische Unterhaltungen (2002). Eigene Notizen zu dieser Nacherzählung hier.