Vor zehn Jahren verstarb mein akademischer Lehrer Professor Peter Brix (Foto). In seinem Institut für Kernphysik an der TU Darmstadt war ich lange Zeit tätig. Ein kleiner, persönlicher Rückblick ist da angebracht.
Zumal ich kürzlich in meinen Unterlagen von damals den Entwurf einer Veröffentlichung entdeckte, die mit Optical Isotope Shift and Changes in Nuclear Mean Square Radius überschrieben war. Der Artikel sollte ein Review der bis dahin (1966) erschienen Arbeiten auf dem Gebiet der optischen Isotopieverschiebung werden. Auf diesem Forschungsgebiet arbeitete Professor Brix vor seiner Berufung nach Darmstadt, zusammen mit seinem Lehrer Kopfermann. In Darmstadt setzte er sich mit Erfolg dafür ein, dort einen Elektronen-Linearbeschleuniger zu installieren und gründete eine Forschungsgruppe, die sich mit der Streuung von Elektronen an Atomkernen beschäftigte. Gleichzeitig weitete er die Untersuchungen zur Isotopieverschiebung auf myonische Atome aus, die Experimente dazu wurden am Europäischen Kernforschungszentrum (CERN) in Genf gemacht.
An dem Review durfte ich mitarbeiten, obwohl ich von optischer Isotopieverschiebung so gut wie keine Ahnung hatte. Eine Ehre für mich, denn ich war damals noch ein Lehrling in der Zunft der Physiker: Meine Diplomarbeit, die ich gerade abgeschlossen hatte, betraf Experimente am Elektronenbeschleuniger. Die hatten keinerlei Bezug zur optischen Spektroskopie. Meine Aufgabe bestand dann auch nur darin, bei der Literaturrecherche zu helfen. Ich sollte alle veröffentlichten Daten zur Isotopieverschiebung sammeln und geeignet darstellen. Als Darstellung hatte sich in der Literatur das so genannte Brix-Kopfermann-Diagramm1 durchgesetzt – der Name lässt erkennen, wer damals das Forschungsgebiet weltweit anführte und Standards setzte. Im Brix-Kopfermann-Diagramm wird die Verschiebung der optischen Spektrallinien für ein Isotopenpaar bezogen auf eine Standard-Verschiebung. Das ist die Verschiebung, die man für Atomkerne mit konstanter Ladungsverteilung berechnet, deren Radius mit der dritten Wurzel aus der Massenzahl ansteigt. Diese Größe, in der Abbildung mit βCexp/Cth bezeichnet, wird als Funktion der Neutronenzahl N des schwereren der beiden Isotope aufgetragen. Für die meisten Isotopenpaare ist βCexp/Cth kleiner als 1, das heißt kleiner als für Standard-Atomkerne erwartet. Es gibt jedoch Ausnahmen im Bereich der Seltenen Erden. Dort ist dieser Wert größer als 1 und deutet damit auf große Unterschiede in der Deformation (Abweichung von der Kugelgestalt) der Isotopenpaare hin.
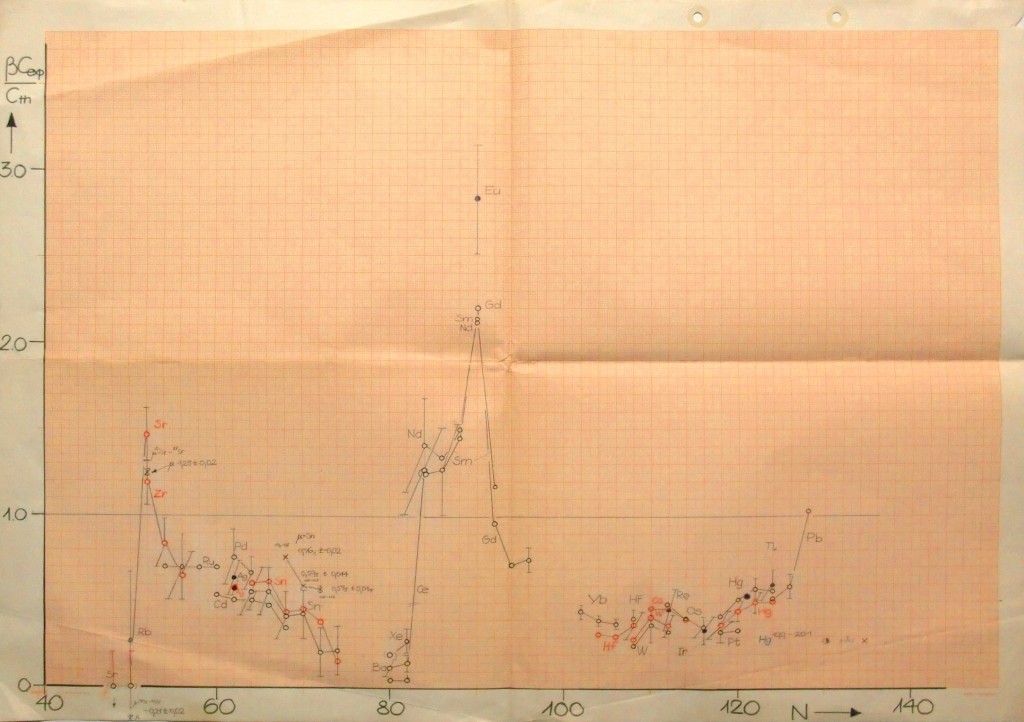Der Review wurde leider nicht fertiggestellt. Ein englischer Kollege kam uns mit einem umfassenden Rückblick zuvor. Von unserem Entwurf überlebten nur ein paar Schreibmaschinen-Durchschläge mit hineingekritzelten Korrekturen – und das Millimeterpapier mit den Isotopieverschiebungen (Abbildung), die ich bis zum Abbruch der Arbeit gesammelt hatte: Mein persönliches Brix-Kopfermann-Diagramm. Inzwischen überholt, aber ein schönes und passendes Andenken an meinen wissenschaftlichen Lehrer.
Ein anderer Review, den ich einige Jahre später (1972) unter Anleitung von Professor Brix schrieb, wurde dann aber wirklich veröffentlicht. Er betraf die Arbeiten zur unelastischen Elektronenstreuung bei niedrigen Energien2, die bis dato bekannt waren. Die meisten von ihnen wurden am Darmstädter Beschleuniger ausgeführt, an einigen dieser Arbeiten war ich beteiligt. In erster Linie beschäftigte ich mich jedoch mit elastischer Elektronenstreuung. Mit dieser Methode bestimmt man mittlere quadratische Kernradien. Ich versuchte, Kernradiusdifferenzen zwischen Isotopen zu messen – also genau die Größe, die man aus den Daten der optischen Isotopieverschiebung gewinnt. Bei den Isotopen, die ich untersuchte, waren die Kernradiusdifferenzen jedoch so klein, dass ich nur eine obere Grenze angeben konnte.
Heute denke ich mit Wehmut an die Zeit im Institut für Kernphysik zurück. Es war nicht nur in wissenschaftlicher, sondern auch in menschlicher Hinsicht ein Ort, an dem man gerne arbeitete.
1 Brix, P. und H. Kopfermann: Physical Review 85, 1050 (1952) und Reviews of Modern Physics 30, (1958), S. 517
2 H. Theissen: Nuclear Spectroscopy of Light Nuclei by Low Energy Inelastic Electron Scattering, Springer Tracts in Modern Physics 65, S. 1 (1972).